Not wrapping the pdf in an ImageObject() will keep the vectors.
newPage()
image('some.pdf', (0,0))
Not wrapping the pdf in an ImageObject() will keep the vectors.
newPage()
image('some.pdf', (0,0))
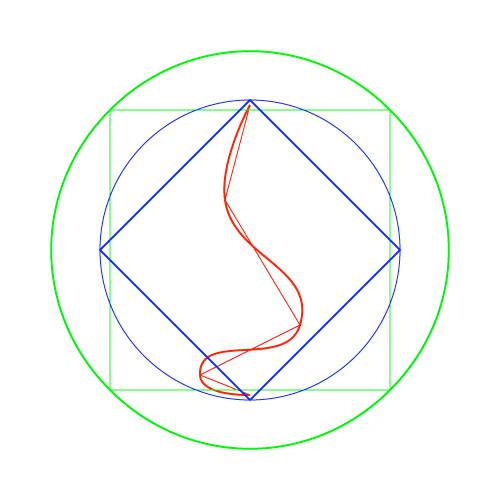
The code responsible for the rounding of the paths in a small animation I made.
DEBUG = False
# A path has points.
# A point has only an anchor [(x,y)], or has an anchor and in and out point [(x,y), (x,y), (x,y)].
# To close a path, repeat the first point at the last position.
jagged_line =[[(500,210)], [(400,250)], [(600,350)], [(450,600)], [(500,790)]]
rectangle =[[(220,220)], [(780,220)], [(780,780)], [(220,780)], [(220,220)]]
circle = [[(500.0, 800.0), (335.0, 800.0), (665.0, 800.0)], [(800.0, 500.0), (800.0, 665.0), (800.0, 335.0)], [(500.0, 200.0), (665.0, 200.0), (335.0, 200.0)], [(200.0, 500.0), (200.0, 335.0), (200.0, 665.0)], [(500.0, 800.0), (335.0, 800.0), (665.0, 800.0)]]
def draw(path):
bez = BezierPath()
bez.moveTo(path[0][0])
for i in range(1, len(path)):
p0 = path[i-1]
p1 = path[i]
if len(p0) == 1 and len(p1) == 1:
# straight line between points
bez.lineTo(p1[0])
elif len(p0) == 3 and len(p1) == 1:
# from curve point to straight point
bez.curveTo(p0[2], p1[0], p1[0])
elif len(p0) == 1 and len(p1) == 3:
# from straight point to curve point
bez.curveTo(p0[0], p1[1], p1[0])
elif len(p0) == 3 and len(p1) == 3:
# curve point on both sides
bez.curveTo(p0[2], p1[1], p1[0])
if path[-1] == path[0]:
bez.closePath()
drawPath(bez)
def round_corners(path, roundness):
if len(path) > 2:
new_path = []
new_path.append(path[0])
new_path.append(path[1])
for i in range(1, len(path) - 1):
p1 = new_path[i - 1]
p2 = path[i]
p3 = path[i + 1]
p1, p2, p3 = round_segment(p1, p2, p3, roundness)
new_path[i - 1] = p1
new_path[i] = p2
new_path.append(p3)
# If the path is closed, we need (the handle of) the first point
if path[-1] == path[0]:
p1 = new_path[-2]
p2 = path[0]
p3 = new_path[1]
p1, p2, p3 = round_segment(p1, p2, p3, roundness)
new_path[-2] = p1
new_path[-1] = p2
new_path[0] = p2
return new_path
else:
return path
def round_segment(p1, p2, p3, roundness):
if roundable(p1, p2, p3):
p2_in, p2_out = create_handles(p1[0], p2[0], p3[0], roundness)
p2 = [p2[0], p2_in, p2_out]
return p1, p2, p3
def roundable(p1, p2, p3):
# If two of the three points are in the same spot,
# we can’t calculate a curve between two points.
p1_anchor = p1[0]
p2_anchor = p2[0]
p3_anchor = p3[0]
d12 = distance_between(p1_anchor, p2_anchor)
d23 = distance_between(p2_anchor, p3_anchor)
if d12 == 0 or d23 == 0:
return False
else:
return True
def create_handles(A, B, C, smoothness):
# A is the point before point B
# B is the point to create the handles for
# C is the point after point B
d_AB = distance_between(A, B)
d_BC = distance_between(B, C)
# Create an isosceles triangle A, B, p4 based on triangle A, B, C.
# Side B, p4 is the same length as side A, B.
# Side B, p4 has the same direction as side B, C
p4_x = ((C[0] - B[0]) * (d_AB / d_BC)) + B[0]
p4_y = ((C[1] - B[1]) * (d_AB / d_BC)) + B[1]
p4 = (p4_x, p4_y)
if DEBUG:
draw_handle(B, p4)
# Calculate a point p5 on the base of the isosceles triangle,
# exactly in between A and B.
p5_x = A[0] + ((p4[0] - A[0]) / 2)
p5_y = A[1] + ((p4[1] - A[1]) / 2)
p5 = (p5_x, p5_y)
if DEBUG:
draw_point(p5, 10)
draw_line(A, p4)
# The line from the top of the isosceles triangle B to
# the point p5 on the base of that triangle
# divides the corner p1, p2, p3 in two equal parts
if DEBUG:
draw_line(B, p5)
# Direction of the handles is perpendicular
vx = p5[0] - B[0]
vy = p5[1] - B[1]
handle_vx = 0
handle_vy = 0
if vx == 0 and vy == 0:
# The three points are on one line, so there will never be a curve.
pass
elif vx == 0:
# prevent a possible division by 0
handle_vx = 1
handle_vy = 0
elif vy == 0:
# prevent a possible division by 0
handle_vx = 0
handle_vy = 1
elif abs(vx) < abs(vy):
handle_vx = 1
handle_vy = vx / vy
else:
handle_vx = vy / vx
handle_vy = 1
# Define handles
handle_a = (B[0] + handle_vx, B[1] - handle_vy)
handle_b = (B[0] - handle_vx, B[1] + handle_vy)
# The handle closest to point A will be the incoming handle of point B
d_ha_A = distance_between(A, handle_a)
d_hb_A = distance_between(A, handle_b)
# I have to make this better. Also, where’s that 0.8 coming from? What was I thinking?
incoming_handle_lenght = d_AB * smoothness
outgoing_handle_length = d_BC * smoothness
total_handle_length = incoming_handle_lenght + outgoing_handle_length
max_handle_length = 0.8 * total_handle_length
if incoming_handle_lenght > max_handle_length:
outgoing_handle_length += incoming_handle_lenght - max_handle_length
incoming_handle_lenght = max_handle_length
if outgoing_handle_length > max_handle_length:
incoming_handle_lenght += outgoing_handle_length - max_handle_length
outgoing_handle_length = max_handle_length
# finally, the in and out points
if d_ha_A < d_hb_A:
B_incoming = (B[0] + handle_vx * incoming_handle_lenght, B[1] - handle_vy * incoming_handle_lenght)
B_outgoing = (B[0] - handle_vx * outgoing_handle_length, B[1] + handle_vy * outgoing_handle_length)
else:
B_incoming = (B[0] - handle_vx * incoming_handle_lenght, B[1] + handle_vy * incoming_handle_lenght)
B_outgoing = (B[0] + handle_vx * outgoing_handle_length, B[1] - handle_vy * outgoing_handle_length)
if DEBUG:
draw_point(B_incoming, 6)
draw_point(B_outgoing, 6)
draw_line(B, B_incoming)
draw_line(B, B_outgoing)
draw_line(A, B)
return B_incoming, B_outgoing
def distance_between(p1, p2):
dx = p2[0] - p1[0]
dy = p2[1] - p1[1]
return pow((dx * dx + dy * dy), 0.5)
def draw_point(point, size):
with savedState():
fill(0, 0.7, 1)
stroke(None)
oval(point[0] - 0.5 * size, point[1] - 0.5 * size, size, size)
def draw_line(a, b):
with savedState():
fill(None)
strokeWidth(1)
stroke(0, 0.7, 1)
line((100, 100), (900, 900))
line(a, b)
def draw_handle(p, h):
draw_point(p, 9)
draw_line(p, h)
fill(None)
# Drawing the original shape and the rounded shape, slightly thicker.
stroke(1, 0, 0)
strokeWidth(2)
draw(jagged_line)
rounded_line = round_corners(jagged_line, 0.4)
strokeWidth(4)
draw(rounded_line)
# A rounding of 0.28 seems to get me as close to a circle as I can get.
stroke(0, 1, 0)
strokeWidth(2)
draw(rectangle)
rounded_rectangle = round_corners(rectangle, 0.28)
strokeWidth(4)
draw(rounded_rectangle)
# Rounding an oval by zero results in a rhombus.
stroke(0, 0, 1)
strokeWidth(2)
draw(circle)
rounded_circle = round_corners(circle, 0)
strokeWidth(4)
draw(rounded_circle)
@rohernandezz You don’t have ~/Library/Preferences/com.drawbot.plist ?
I don’t believe it’s possible with DrawBot’s Variables.
It might be possible to use DrawBot with Vanilla and create your own interface, but I have no first hand experience with that.
Also, the example script on that page does only work for me if I add this at the top:
from PyObjCTools import AppHelper
and this at the bottom:
AppHelper.runEventLoop()
areaAverage() does not return anything, but changes the imageObject.
p = 'schrofer_head.jpg'
im = ImageObject(p)
print(im.size()) # (1365.0, 1365.0)
im.areaAverage()
print(im.size()) # (1.0, 1.0)
print(imagePixelColor(im, (0, 0))) # (0.6, 0.6039215686274509, 0.6, 1.0)
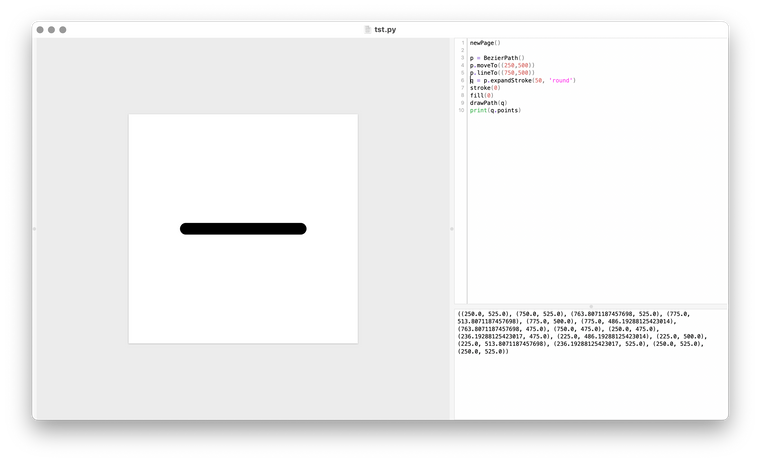
Hi Maurice, expandStroke() returns a path.
Almost the same code, but instead of drawing a grid we draw 1000 circles randomly. As they have to stay in the same place, we save their locations in an array.
(Also in this script some nice code to have if you want to publish animated gifs; a way to reduce the colours in the gif.)
import random
import struct
frames = 24
page_size = 1000
number_of_circles = 1000
min_dot_size = 10
max_dot_size = 70
radius = 200
# create color table for gif
# https://stackoverflow.com/questions/6269765/what-does-the-b-character-do-in-front-of-a-string-literal
table = b""
greys = [0,85,170,255]
for i in greys:
r = struct.pack(">B", i)
g = struct.pack(">B", i)
b = struct.pack(">B", i)
table += r + g + b # + a
def draw_dot(center, diameter):
x = center[0] - diameter / 2
y = center[1] - diameter / 2
oval(x, y, diameter, diameter)
# Generate circles, randomly distributed
circles = []
for i in range(number_of_circles):
x = random.randint(0,page_size)
y = random.randint(0,page_size)
circles.append((x,y))
for f in range(frames):
percentage_animated = f / frames
newPage()
fill(0)
rect(0, 0, page_size, page_size)
for c in circles:
x = c[0]
y = c[1]
distance = pow( (pow(x - page_size / 2, 2 ) + pow(y - page_size / 2, 2)), 0.5)
distance = distance - percentage_animated * radius * 2
distance = distance % (radius * 2)
percentage = distance / radius
if percentage > 1:
percentage = 2 - percentage
dot_size = min_dot_size + percentage * (max_dot_size - min_dot_size)
fill(None)
stroke(1)
draw_dot((x,y), dot_size)
saveImage("animated.gif", imageGIFRGBColorTable = table)

frames = 24
page_size = 1000
grid_size = 20
grid_spacing = page_size / grid_size
min_dot_size = 10
max_dot_size = 50
radius = 100
def draw_dot(center, diameter):
x = center[0] - diameter / 2
y = center[1] - diameter / 2
oval(x, y, diameter, diameter)
for f in range(frames):
percentage_animated = f / frames
newPage()
fill(0)
rect(0, 0, page_size, page_size)
for row in range(grid_size):
for column in range(grid_size):
x = row * grid_spacing + grid_spacing / 2
y = column * grid_spacing + grid_spacing / 2
# Calculate distance from (x,y) of the dot to the center of the page
distance = pow( (pow(x - page_size / 2, 2 ) + pow(y - page_size / 2, 2)), 0.5)
# The wave must seem to move, so for every frame in the
# animation, add a precentage of the length of the wave.
# Add or substract to change direction.
distance = distance - percentage_animated * radius * 2
# Use modulo to get a distance between 0 and double the radius
distance = distance % (radius * 2)
# The wave has a lenghth of double the radius. In the
# first halve of the lenght, the dots get larger, in the
# second halve the dots get smaller.
# So, we calculate a percentage between 0 and 2, and when
# the percentage is larger than 1, we count backwards.
percentage = distance / radius
if percentage > 1:
percentage = 2 - percentage
dot_size = min_dot_size + percentage * (max_dot_size - min_dot_size)
fill(1)
draw_dot((x,y), dot_size)
saveImage("animated.gif")
You could combine that with bitmapFont-Drawbot.py from Connor Davenport, which will give you something like this:

Do you mean something like this?
w = 1920
h = 1080
columns = 13
spacing = w/(columns+1)
fs = 60
duration = .25
txt = 'ABCD'
frames = columns+len(txt)+1
for frame in range(frames):
newPage(w, h)
frameDuration(duration)
fontSize(fs)
# white background
with savedState():
fill(1)
rect(0,0,w,h)
for column in range(columns):
x = spacing + column * spacing
# Use the frame count as starting position for the text.
# frame-len(txt) makes sure the start of the text is outside the row of characters
if column >= frame-len(txt) and column < frame:
# txt[0] gets the first character, A, txt[1] gets the second, etc.
# txt[column-frame] makes sure the range alway stays between 0 and the length of the text,
# as the length of frames is defined by columns+len(txt)+1.
text(txt[column-frame], (x, h/2), align='center')
else:
# If the column position is not between frame-len(txt) and frame, use a dot.
# You could add random characters here.
text('.', (x, h/2), align='center')
saveImage('abcd.gif')
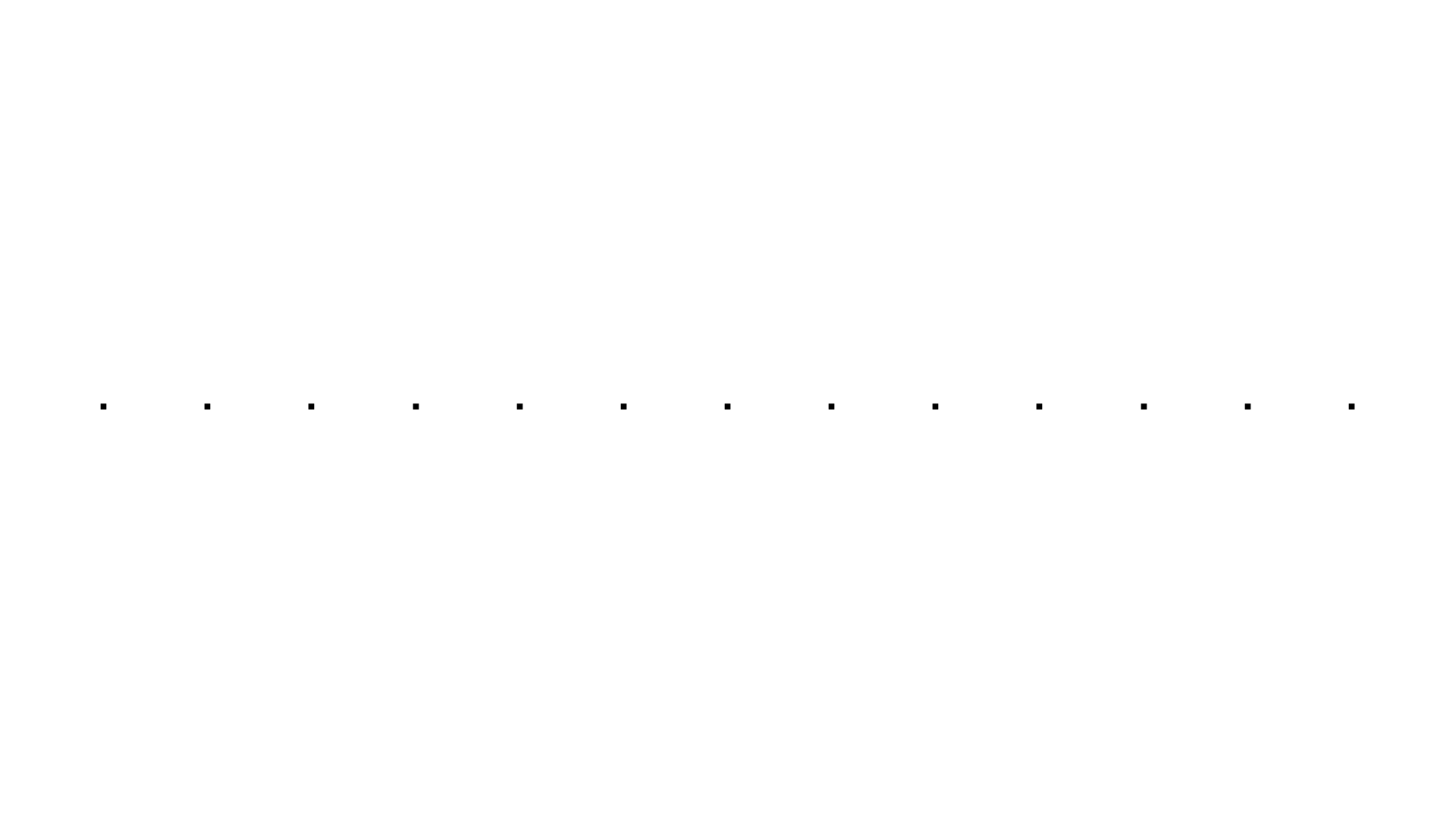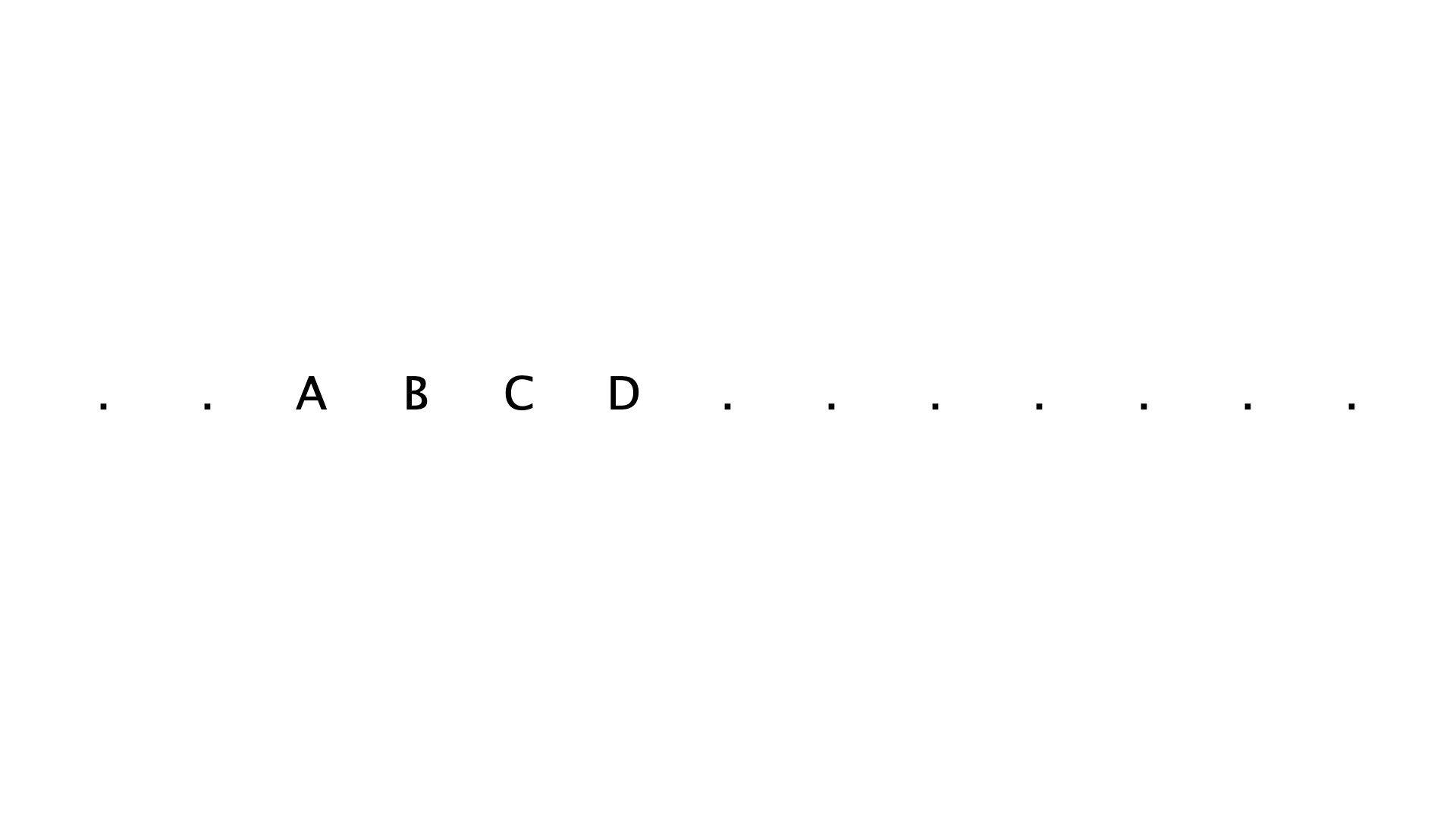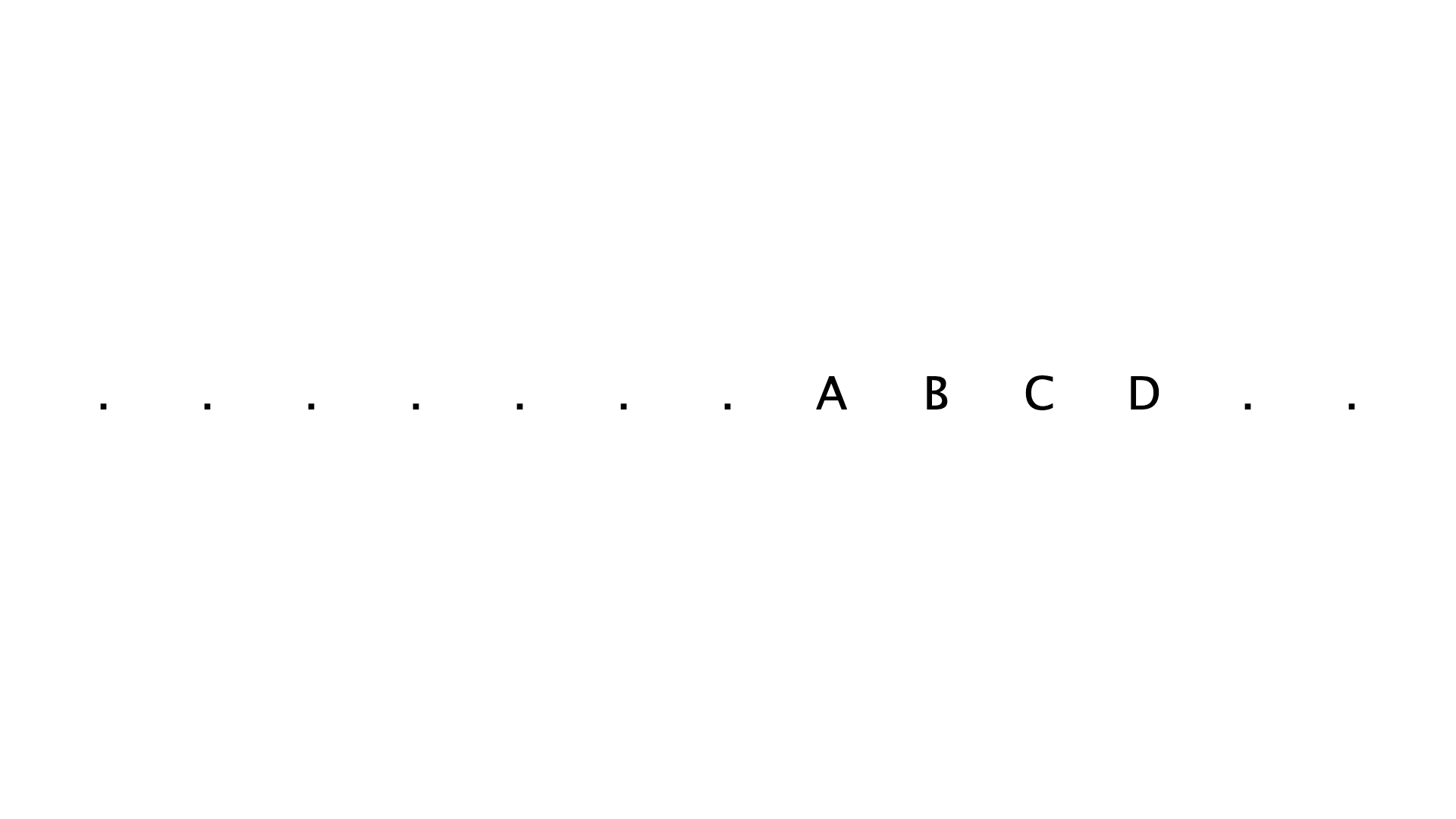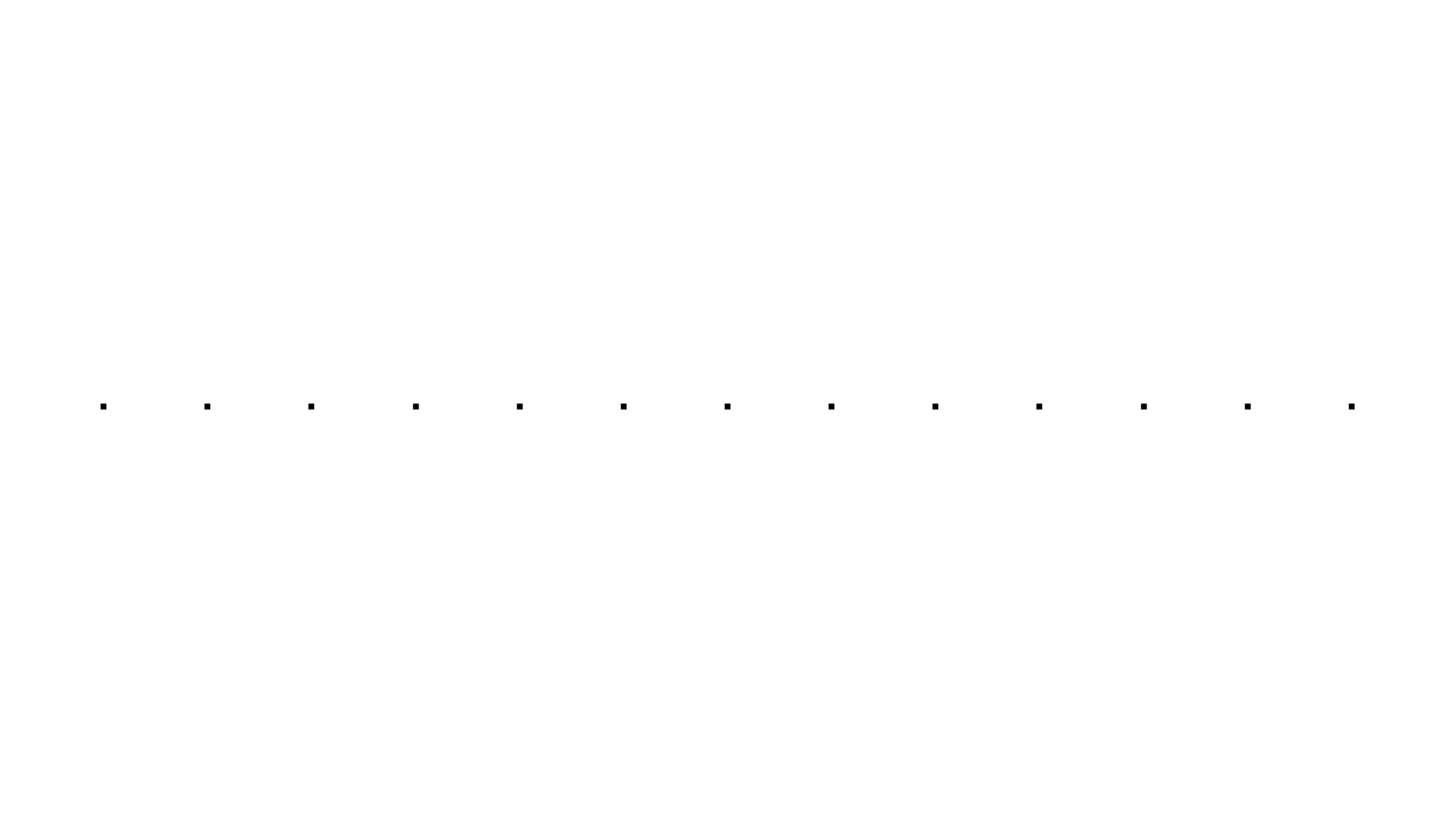
You are correct, I should have looked better.
I don’t know if there exist these kind of filters for DrawBot (I assume you mean something like Illustrator’s Pathfinder tool).
I did some reading on the underlying NSBezierPath, which has an even-odd winding rule, but I'm not smart enough to figure out if that's useable, let alone how.
Nice! Thanks for sharing the result.
I think you ask for something from DrawBot that is not there.
formattedString = FormattedString('HO', font='Helvetica', fontSize=700)
# Get the Bézier path of the text using FormattedString
path = BezierPath()
path.text(formattedString, (50, 50))
# Draw the bezier path with the formatted string
newPage()
with savedState():
fill(.8)
drawPath(path)
# A segment of a DrawBot contour doesn’t have an attribute ‘points’ or ‘type’
for contour in path.contours:
for segment in contour:
print(segment) # returns list with point(s)
print(type(segment)) # returns ‘<class 'list'>’
# print(segment.points) # returns AttributeError: 'list' object has no attribute 'points'
# print(segment.type) # returns AttributeError: 'list' object has no attribute 'type'
if hasattr(segment, 'points'):
# Will never be true
print(segment.points)
Not sure if this is completely correct and robust enough for what you need, but it works. At least for H and O.
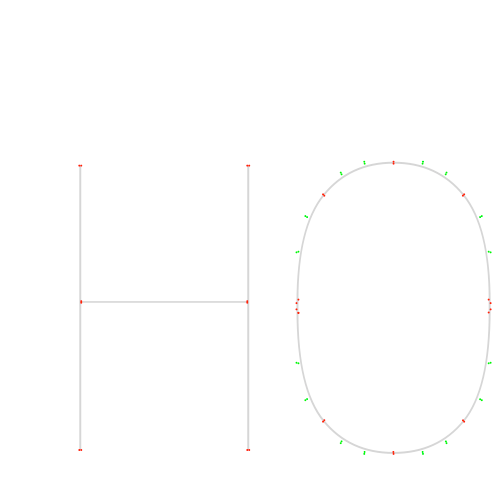
# Set up canvas
canvas_width = 500
canvas_height = 500
txt = "HO"
variable_font_path = "RobotoFlex-VariableFont_GRAD,XOPQ,XTRA,YOPQ,YTAS,YTDE,YTFI,YTLC,YTUC,opsz,slnt,wdth,wght.ttf"
font_size = 400
point_size = 2
# Neue Seite erstellen und Hintergrund setzen
newPage(canvas_width, canvas_height)
fill(1) # Weißer Hintergrund
rect(0, 0, canvas_width, canvas_height)
fill(0) # Schwarzer Text
# Schriftart setzen und prüfen, ob sie korrekt geladen wird
font(variable_font_path)
fontSize(font_size)
# Alle Achsen der aktuellen Schriftart auflisten
variations = listFontVariations()
# for axis, data in variations.items():
# print(f"Axis: {axis}, Data: {data}")
# Eine Variation der aktuellen Schriftart auswählen
if 'wght' in variations:
fontVariations(wght=500)
# Create a FormattedString with the text and variable font
formattedString = FormattedString(txt, font=variable_font_path, fontSize=font_size)
# Get the Bézier path of the text using FormattedString
path = BezierPath()
path.text(formattedString, (50, 50))
with savedState():
fill(.8)
drawPath(path)
# Initialize lists to hold on-curve and off-curve points
on_curve_points = []
off_curve_points = []
# Iterate through contours and segments to extract points
output = ""
for contour in path.contours:
# moveTo
x, y = contour[0][0]
on_curve_points.append((x, y))
for segment in contour[1:]:
if len(segment) == 1:
# lineTo
pt = segment[0]
on_curve_points.append((pt[0], pt[1]))
if len(segment) == 3:
# curveTo
cp1 = segment[0]
cp2 = segment[1]
pt = segment[2]
off_curve_points.append((cp1[0], cp1[1]))
off_curve_points.append((cp2[0], cp2[1]))
on_curve_points.append((pt[0], pt[1]))
# Draw on-curve points
fill(1, 0, 0) # Rot für on-curve Punkte
stroke(None)
for (x, y) in on_curve_points:
print("Drawing on-curve point at:", x, y)
oval(x - point_size / 2, y - point_size / 2, point_size, point_size)
# Draw off-curve points
fill(0, 1, 0) # Grün für off-curve Punkte
stroke(None)
for (x, y) in off_curve_points:
print("Drawing off-curve point at:", x, y)
oval(x - point_size / 2, y - point_size / 2, point_size, point_size)
# Save the image
saveImage("H_with_anchor_points.png")
# Ausgabe der Koordinaten
print(output)
I’m trying to understand the problem. Does this simplification work with your font?
What I'd like to do is keep fontSize constant and vary the lineHeight from line to line […]
source = 'lestextessociologiques'
fSize = 90
array = FormattedString()
ft = 'Helvetica'
lh_min = 100
lh_max = 200
lh_step = 10
temp = FormattedString()
for lh in range(lh_min, lh_max, lh_step):
temp.append(source, font=ft, fontSize=fSize, lineHeight=lh, align='center')
temp.append('\n')
array.append(temp)
newPage()
with savedState():
fill(1)
rect(0, 0, width(), height())
textBox(array, (0, 0, width(), height()))
fill(None); stroke(1, 0, 0)
y = height()
for lh in range(lh_min, lh_max, lh_step):
y -= lh
line((0, y), (width(), y))
saveImage('~/Desktop/baseline_test.png')

You could create an imageObject of the background, but I believe you get pixels instead of outlines.
Maybe you can create the whole background in one BezierPath? I’m not sure, but it seems possible to append multiple paths to one BezierPath.
I don’t believe it’s possible with DrawBot’s Variables.
It might be possible to use DrawBot with Vanilla and create your own interface, but I have no first hand experience with that.
Also, the example script on that page does only work for me if I add this at the top:
from PyObjCTools import AppHelper
and this at the bottom:
AppHelper.runEventLoop()
The thing that tripped me up initially was ‘Returns a single-pixel image…’. I was (mis)reading that and assumed that ‘returns’ meant ‘returns a new image’ instead of altering the imageObject.
I’m not sure if the documentation is a little confusing, or that the behaviour of areaAverage is unexpected.
@micahmicah Maybe, if the last segment is a line, the last point is not updated?
Maybe change:
# IF IT'S A LINE DRAW A LINE
if len(segment) == 1:
x,y = segment[0].x, segment[0].y
P.lineTo((x,y))
#SHOW POINTS
rect(x-diameter/2,y-diameter/2,diameter,diameter)
to:
# IF IT'S A LINE DRAW A LINE
if len(segment) == 1:
x3,y3 = segment[0].x, segment[0].y
P.lineTo((x3,y3))
#SHOW POINTS
rect(x3-diameter/2,y3-diameter/2,diameter,diameter)
(I’m coding blind, I have not tested this)