After a request to add more axes to the previous simple variable fonts tutorial the follow up escalated a bit. Since there are several files I thought it might be better to put them on github.
jo
@jo
Best posts made by jo
-
More variable fonts nonsenseposted in Code snippets
-
Rotating rectangles based on an artpiece by Vera Molnarposted in Tutorials
Intro
This is based on an art work by Vera Molnar (a pioneer in the field of generative art).
This script will generate a pattern with randomly rotated rectangles – using two nested loops.Code and explanation
Lets start with the default settings of DrawBot:
fill color is black, a white background and a canvas with a width and height of 1000 units.First we define how many rows and columns we want to have in the drawing and assign this value to the variable amount
amount = 24Next we want to define the size of each cell in the grid. We want to calculate this value and not define a fixed value so it updates automatically. To calculate the width of the cell we call the width() function which returns the width of the canvas (in our case the default value of 1000). We divide this value by the amount of cells (stored in the variable amount). Since we want to have a margin around the drawing we just add 2 to the amount.
cell_s = width() / (amount + 2)Since we want the squares rotated by 45 degrees to touch at the corners we need to calculate the size of the rectangles.
With a rotation of 45 degrees this can be done quite easily by dividing the cell size by the square root of 2.rect_s = cell_s / sqrt(2)Now we should have all the numbers ready to start drawing the pattern. To apply the margin we first shift the origin of the drawing one cell size to the right and to the top. We do this by calling the translate() function with the parameters of one cell size in the x direction and the y direction
translate(cell_s, cell_s)Now lets start to loop in the x direction as many times as defined in the amount variable
for x in range(amount):And then for each x value do the same in the y direction. So our total amount of cells will be the square of the amount (24 * 24 = 576 cells).
for y in range(amount):Before we call the rotate() function lets first shift the origin with the translate() function. Since we want to revert back to the default state (with no rotation) after we have drawn a rectangle let’s call the savedState() function first:
with savedState():Now let’s do the shifting: Shift x times the cell size to the left and y times the cell size to the top. Since we want the rotation to be happening in the center of the cell we need to add half a cell size in each direction.
translate( x * cell_s + cell_s/2, y * cell_s + cell_s/2 )We only want to do the rotation on some of the cells. So we just call the random() function which returns a randomly generated value between 0 and 1. If this value is higher than 0.5 (which on average should be in half of the cases) let’s do the rotation:
if random() > .5: rotate(45)Finally lets draw a rectangle by calling the rect() function. The rectangle should be drawn half a cell size to the left and bottom to compensate for the extra translation from before:
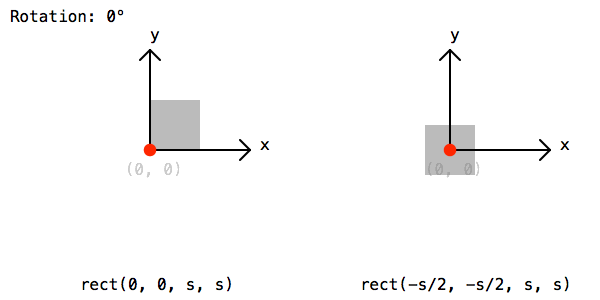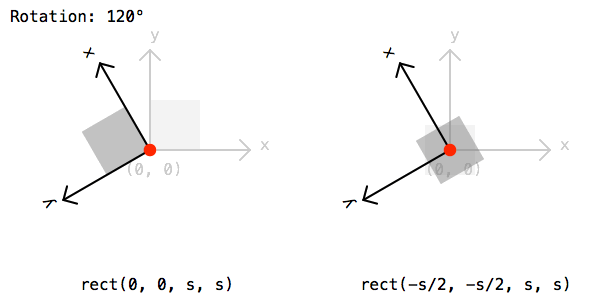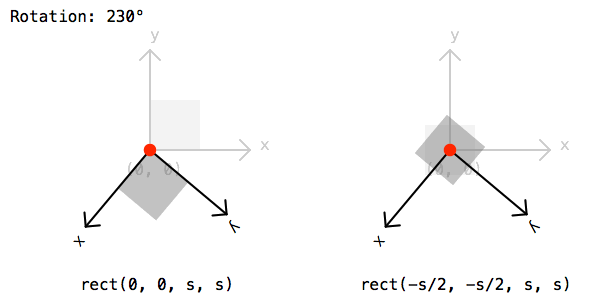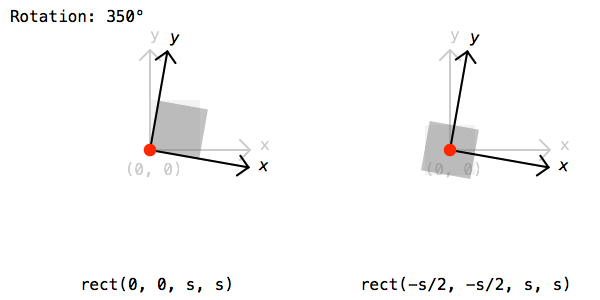
rect(-rect_s/2, -rect_s/2, rect_s, rect_s)To save the image lets call the saveImage() function and give a path and file name:
saveImage('~/Desktop/Vera_Molnar_rotating_rects.png')Everything put together
amount = 24 cell_s = width() / (amount + 2) rect_s = cell_s / sqrt(2) translate( cell_s, cell_s) for x in range(amount): for y in range(amount): with savedState(): translate( x * cell_s + cell_s/2, y * cell_s + cell_s/2 ) if random() > .5: rotate(45) rect(-rect_s/2, -rect_s/2, rect_s, rect_s) # saveImage('~/Desktop/Vera_Molnar_rotating_rects.png')Image

-
Vera Molnar re-codedposted in Code snippets
Vera Molnar is a great computer generated arts pioneer and is still working. I could not resist to emulate and try to recode some of her artworks. Using drawbot to do so is great fun and pretty easy — one can only wonder about the struggles she had to overcome. With all due respect here is a link to github with my humble attempts.
-
Animated Müller-Lyer illusionposted in Code snippets
nautil.us has a nice blogpost of optical illusions. I could not resist the attempt to build one of them in drawbot.
pw = ph = 400 # define variables to set width and height of the canvas cols = 14 # define how many columns there should be rows = 4 # define how many rows there should be pages = 30 # define how many frames the gif should have. more pages mean slower movement angle_diff = 2 * pi/pages # we want the loop to make one full circle. 2 times pi is 360 degrees. Divided by the amount of pages this gives us the angle difference between pages. gap = pw/(cols+1) # calculate the gap between the lines. l = (ph - 2 * gap)/rows # calculate the length of the line. for p in range(pages): newPage(pw, ph) translate(gap, gap) fill(None) strokeWidth(2) for x in range(cols): y_off = cos( 3 * pi * x/cols + angle_diff * p ) * gap/2 # calculate how high or low the arrowhead should be for y in range(rows+1): stroke(1,0 ,0) if y % 2 == 0 else stroke(0, 0, 1) if y < rows: line((x*gap, y*l), (x*gap, y*l+l)) stroke(0) y_off *= -1 # switch to change direction line( (x*gap, y*l), (x*gap - gap/2, y*l - y_off) ) line( (x*gap, y*l), (x*gap + gap/2, y*l - y_off) ) # saveImage('~/Desktop/opti_illu.gif')this should generate something like this:
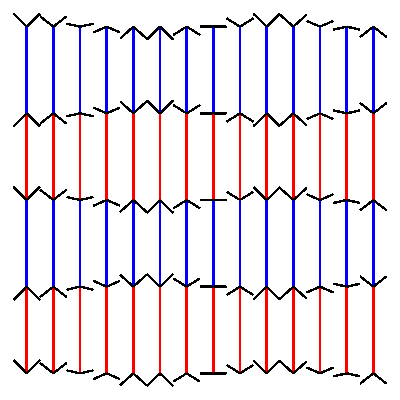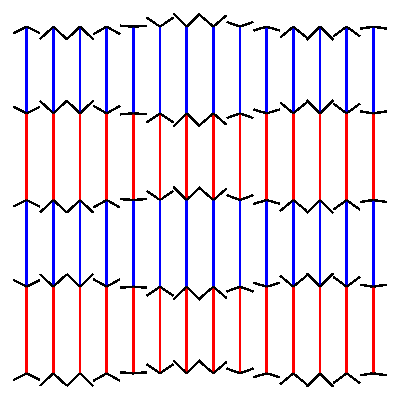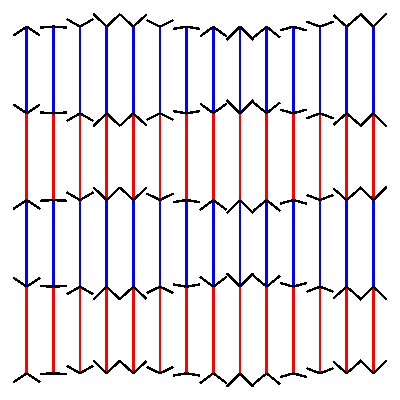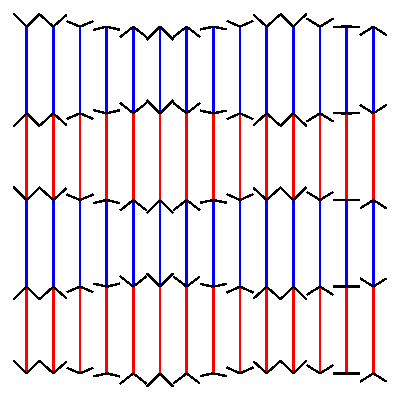
-
RE: Cellular automatonposted in Code snippets
the script could be used to get a scarf knitted.
good idea. thanks for the tipp @frederikrule 122 on one side which makes the other side rule 161

-
RE: How to mirror/flip a object?posted in General Discussion
the mirrored drawing is probably happening outside your canvas. keep in mind that every transformation (scale, skew, rotation, etc) is always starting from the origin. so a mirroring from the default origin (left, bottom corner) will be to the left or below your canvas. see the example below with a shifted origin.
pw = 1000 ph = 400 txt = "SHADE" newPage(pw, ph) translate(0, 160) # shift the origin up a bit fontSize(300) text(txt, (pw/2, 0), align = 'center') scale(x=1, y=-.5) # the mirroring text(txt, (pw/2, 0), align = 'center') -
RE: A deeper bevel on lineJoin()?posted in General Discussion
@mauricemeilleur I don’t know how Crouwel defined his rules. but to me the corner-rule seems like an integral part of the design.
I had a look at my code and tried to tidy the worst bits. some of the angle calculations seem very inefficient but ¯\(ツ)/¯ here it is:
EDIT 2018-05-28 changed the code to simplify some of the horrible trigonometry and there now is the
sq_capbool to have squared linecaps.# Draw a 'folded outline' between a set of points. # TO DO: There should be an error message when two dots are closer to each other and the weight. # There should be a warning if the folding is further than the next points. # There should be a warning for collinear points. import math # Just a bunch of points p01 = (894, 334) p02 = (808, 86) p03 = (274, 792) p04 = (481, 920) p05 = (583, 730) p06 = (85, 430) p07 = (318, 100) p08 = (870, 600) p09 = (720, 690) points = [p01, p02, p03, p04, p05, p06, p07, p08, p09] def get_dist(p1, p2): return sqrt( (p2[0] - p1[0] )**2 + (p2[1] - p1[1])**2 ) def calc_angle(p1, p2): return atan2((p2[1] - p1[1]), (p2[0] - p1[0])) def calc_delta(p1, p2, p3): ''' Returns the angle between three points. ''' return calc_angle(p2, p3) - calc_angle(p2, p1) def calc_offset(weight, p1, p2, p3): ''' Returns the x and y "offset" to be added to the points of the polygon. ''' halfWeight = weight/2 if p1 == p2: alpha = calc_angle(p1, p3) b = -sin(alpha) * halfWeight a = cos(alpha) * halfWeight elif p2 == p3: alpha = calc_angle(p1, p3) b = sin(alpha) * halfWeight a = -cos(alpha) * halfWeight else: alpha = calc_angle(p2, p3) delta = calc_delta(p1, p2, p3) xx = halfWeight / sin((delta - pi) / 2) delta_f = (2 * alpha - pi - delta ) / 2 a, b = xx * sin(delta_f), xx * cos(delta_f) return a, b def wrap_line(p1, p2, p3, p4, weight): ''' This draws a polygon around a line. Four points (x,y) and a weight parameter are required. The polygon will be drawn around the two middle points. The first and last points define the angles. ''' a, b = calc_offset(weight, p1, p2, p3) # extend first point x1b, y1b = p2[0] - b, p2[1] - a x1c, y1c = p2[0] + b, p2[1] + a # extend second point c, d = calc_offset(weight, p2, p3, p4) x2b, y2b = p3[0] - d, p3[1] - c x2c, y2c = p3[0] + d, p3[1] + c polygon((x1b, y1b), (x1c, y1c), (x2b, y2b), (x2c, y2c)) # -------------------------------------------------------------------- # The actual drawing fill(0, .4) weight = 180 sq_cap = True if len(points) == 1: rect(points[0][0] - weight/2, points[0][1] - weight/2, weight, weight) for i, point in enumerate(points[:-1]): # print (get_dist(point, points[i+1])) if len(points) == 2: wrap_line(points[i], points[i], points[i+1], points[i+1], weight) else: if i == 0: aaa = calc_angle(points[i], points[i+1]) if sq_cap: point = point[0] - weight/2 * cos(aaa), point[1] - weight/2 * sin(aaa) wrap_line(point, point, points[i+1], points[i+2], weight) elif i == len(points)-2: next_p = points[i+1] aaa = calc_angle(points[i], next_p) if sq_cap: next_p = next_p[0] + weight/2 * cos(aaa), next_p[1] + weight/2 * sin(aaa) wrap_line(points[i-1], points[i], next_p, next_p, weight) else: # print ( calc_delta(points[i-1], points[i], points[i+1]) ) wrap_line(points[i-1], points[i], points[i+1], points[i+2], weight)
-
RE: Tutorial request: how to animate a variable fontposted in Tutorials
hi there
I will try to give you a basic start with a very simple linear interpolation.–––
Let’s animate some variable fonts.
we are on mac os so lets first see if there are any variable fonts installed on the system
To do this lets iterate through all installed fonts and ask if they do have any font variation axes. the function
listFontVariations()will return this information as anOrderedDictif you supply a font name. Let’s print the name of the font if it returns any variable axes. And then let’s iterate through this information (short code and information on the values that could be set) for every axis and print this as well.for fontName in installedFonts(): variations = listFontVariations(fontName) if variations: print(fontName) for axis_name, dimensions in variations.items(): print (axis_name, dimensions) print ()Depending on your os version you should get a few fonts.
Let’s assume one of the fonts is 'Skia-Regular' and it did print the following information:Skia-Regular wght {'name': 'Weight', 'minValue': 0.4799, 'maxValue': 3.1999, 'defaultValue': 1.0} wdth {'name': 'Width', 'minValue': 0.6199, 'maxValue': 1.2999, 'defaultValue': 1.0}This information can now be used to set some typographic parameters. Let’s use the weight axis (wght) and animate from the minimum to the maximum. To do so we assign these two values to variables.
min_val = listFontVariations('Skia-Regular')['wght']['minValue'] max_val = listFontVariations('Skia-Regular')['wght']['maxValue']Let’s also assign the amount of steps for the interpolation to a variable and the text we want to render.
steps = 10 txt = 'var fonts are fun'The last variable we are going to need is a calculation of the stepsize.
So let’s get the range by subtracting the minimum from the maximum and divide this value by the amount of steps minus one step.step_size = (max_val - min_val) / (steps-1)We should now be ready to loop through the amount of steps.
For every step we make a new page and set the font and font size. We calculate the value for the respective step by multiplying the step_size by the step and add it to the minimum value. The result of this calculation is then used in thefontVariations()function to set the variable font values.for i in range(steps): newPage(1100, 200) font("Skia-Regular") fontSize(120) curr_value = min_val + i * step_size fontVariations(wght= curr_value ) text(txt, (70, 70))Everything put together
for fontName in installedFonts(): variations = listFontVariations(fontName) if variations: print(fontName) for axis_name, dimensions in variations.items(): print (axis_name, dimensions) print () min_val = listFontVariations('Skia-Regular')['wght']['minValue'] max_val = listFontVariations('Skia-Regular')['wght']['maxValue'] steps = 10 txt = 'var fonts are fun' step_size = (max_val - min_val) / (steps-1) for i in range(steps): newPage(1100, 200) font("Skia-Regular") fontSize(120) curr_value = min_val + i * step_size fontVariations(wght= curr_value ) text(txt, (70, 70)) fontSize(20) fontVariations(wght= 1 ) text('Weight axis: %f' % curr_value, (10, 10)) saveImage('~/Desktop/var_fonts_interpol.gif')Final gif
With 20 interpolation steps and with a smaller canvas size.

Any questions or corrections please let me know!
-
Lissajous tableposted in Code snippets
Here is some code to draw a Lissajous table.
Change thefunc_xand/orfunc_y(sin or cos) and/or add some value to thedeltato get other curves.
Well, actually the curves are just polygons.# ---------------------- # lissajous table # ---------------------- # settings cols = 12 rows = 8 cell_s = 80 r_factor = .8 # fraction of the cell size to have a gap between them func_x = cos # should be `sin` or `cos` func_y = sin # should be `sin` or `cos` delta = 0 #pi/3 # some angle in radians density = 360 # amount of points per cell – higher values make nicer curve approximations # ---------------------- # calculated settings radius = (cell_s * r_factor) / 2 step = (2 * pi) / density pw = cell_s * (cols + 1) ph = cell_s * (rows + 1) x_coords = { (col, d) : func_x(step * (col + 1) * d + pi/2 + delta) * radius for col in range(cols) for d in range(density) } y_coords = { (row, d) : func_y(step * (row + 1) * d + pi/2) * radius for row in range(rows) for d in range(density) } # ---------------------- # function(s) def draw_cell(pos, col, row): cx, cy = pos points = [(cx + x_coords[(col, f)], cy + y_coords[(row, f)]) for f in range(density)] polygon(*points) # ---------------------- # drawings newPage(pw, ph) rect(0, 0, pw, ph) fontSize(12) translate(0, ph) fill(1) text('δ\n{0:.2f}°'.format(degrees(delta)), (cell_s * (1 - r_factor)/2, -20)) for col in range(1, cols+1): cx = col * cell_s + cell_s * (1 - r_factor)/2 text('{0}\n{1}'.format(func_x.__name__, col), (cx, -20)) for row in range(1, rows + 1): cy = row * cell_s + cell_s * (1 - r_factor) text('{0}\n{1}'.format(func_y.__name__, row), (cell_s * (1 - r_factor)/2, -cy)) fill(None) stroke(.5) strokeWidth(1) for col in range(cols): for row in range(rows): draw_cell((cell_s * col + cell_s * 1.5, - cell_s * row -cell_s * 1.5), col, row)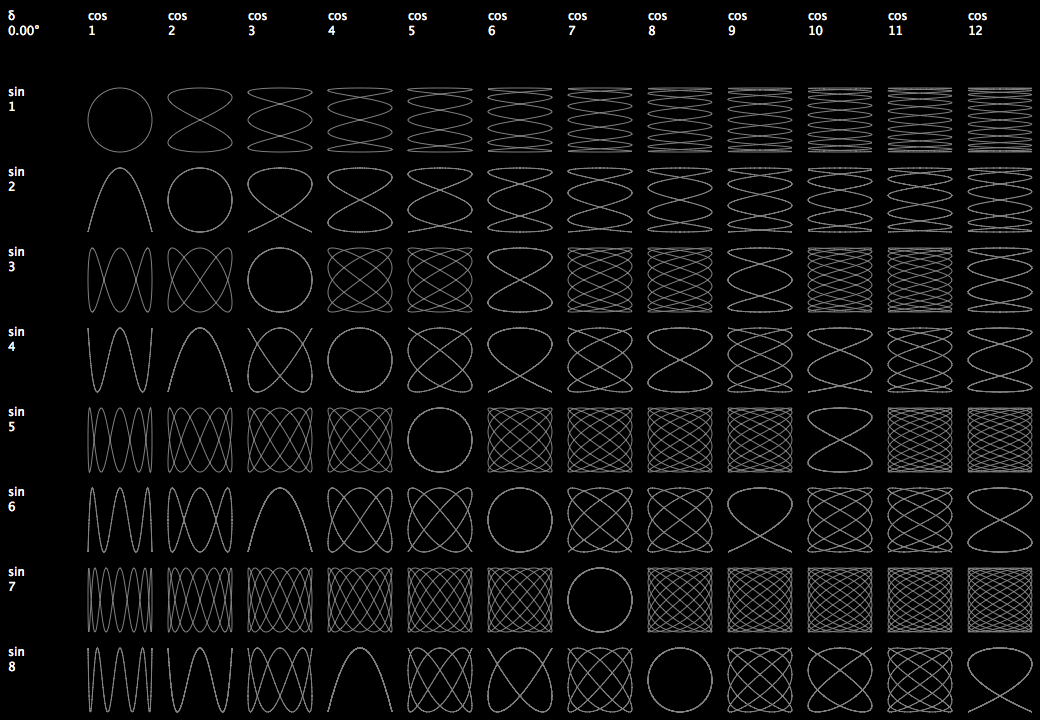
-
Drawing a circle with Beziersposted in Code snippets
You cannot draw a circle with Beziers.
When I first read this some time ago I was a bit confused.
Why is this not a circle. It sure looks like one.After learning a bit more about curve descriptions and calculations I kind of agree but the quote should better say:
You cannot draw a perfect circle with Beziers.
Getting the best tangent values.
We have a formula to calculate points on a Bezier Curve.
x = (1-t)**3*p1[0] + 3*(1-t)**2*t*t1[0] + 3*(1-t)*t**2*t2[0] + t**3*p2[0] y = (1-t)**3*p1[1] + 3*(1-t)**2*t*t1[1] + 3*(1-t)*t**2*t2[1] + t**3*p2[1]p1 and p2 are the two endpoints and t1 and t2 the two tangent points. t is the factor (0-1) at which we want the point on the curve.
On a bezier curve with the following coördinates:
p1 = (1, 0) p2 = (0, 1) t1 = (1, tangent_val) t2 = (tangent_val, 1)we can calculate the tangent_val if we assume that the point at t=0.5 (halfway the curve) is exactly on the circle. Halfway of a quartercircle is 45 degrees so x and y are both at 1/sqrt(2). If we plug these numbers into the formula we can calculate the tangent value:
1/sqrt(2) = (1-.5)**3*1 + 3*(1-.5)**2*.5*1 + 3*(1-.5)*.5**2*tangent_val + .5**3*0 ... tangent_val = 4*(sqrt(2)-1)/3 ≈ 0.5522847493With this tangent_val we can calculate other points on the bezier curve. Of which we can calculate the angle in respect to the center point at (0, 0). And with this angle we can use sine and cosine to get the point that would be on a circle.
We can also calculate the distance of the bezier point and see where the offset is the biggest. As we can see the difference is really tiny. With a radius of 1 the biggest off value is 1.0002725295591013 (not even one permille). The difference is hardly visible so I added only the top part of a really long bar chart to make it show.
See the image below:
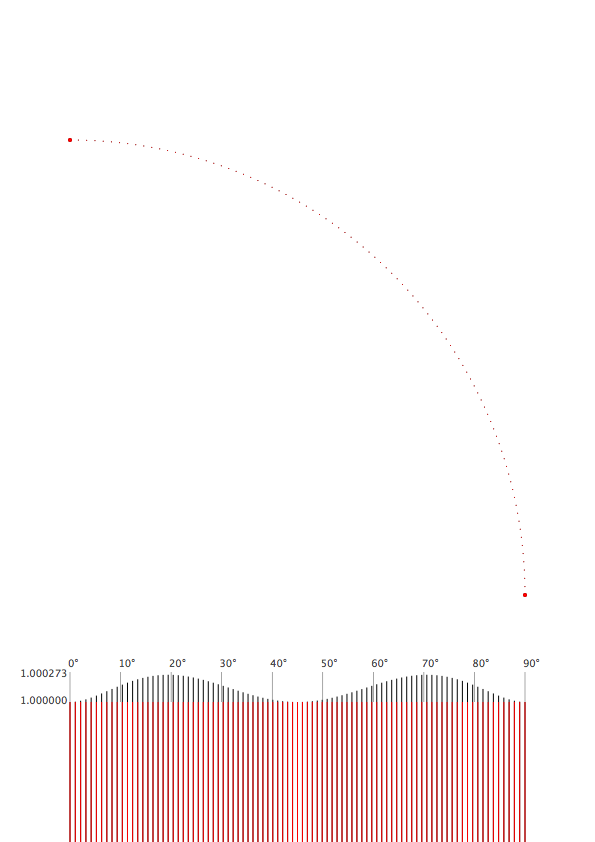
Code
# ------------------- # settings pw, ph = 595, 842 #A4 margin = 70 tang = 4*(sqrt(2)-1)/3 r = pw - 2 * margin density = 90 # amount of points dia_ = 1 # diameter to draw the points r_plot = 100000 # this is a magnifying factor to make the tiny difference visible. r_plot_y = margin - r_plot #radius plotting c_plot_y = ph - 3 * margin - r # circle plotting # ------------------- # functions def get_bezier_p(p1, t1, t2, p2, t): ''' get the point on a bezier curve at t (should be between 0 and 1) ''' x = (1 - t)**3 * p1[0] + 3*(1 - t)**2 * t * t1[0] + 3*(1 - t)* t**2 * t2[0] + t**3 * p2[0] y = (1 - t)**3 * p1[1] + 3*(1 - t)**2 * t * t1[1] + 3*(1 - t)* t**2 * t2[1] + t**3 * p2[1] return x, y def get_dist(p1, p2): ''' returns the distance between two points (x, y)''' return sqrt((p2[0]-p1[0])**2 + (p2[1]-p1[1])**2) # ------------------- # drawings newPage(pw, ph) fill(1) rect(0, 0, pw, ph) translate(margin, margin) # draw the tangent points rect(r - dia_, c_plot_y + tang*r - dia_, dia_*2, dia_*2) rect(tang*r -dia_, c_plot_y + r - dia_, dia_*2, dia_*2) max_off = 1 for i in range(density+1): # ------- # bezier # calculate the factor f f = i/density fill(0) if i == 0 or i == (density): dia = dia_ * 4 else: dia = dia_ # get the coordinates for the point at factor f x_b, y_b = get_bezier_p( (1, 0), (1, tang), (tang, 1), (0, 1), f ) # get the distance of the point from the center at (0, 0) r_b = get_dist((0, 0), (x_b, y_b)) max_off = max(max_off, r_b) # get the angle of the point angle = atan2(y_b, x_b) # draw the point and a rect for the bar chart oval(x_b * r - dia/2, c_plot_y + y_b * r - dia/2, dia, dia) rect((angle/(pi/2)) * r - dia_/2, r_plot_y, dia_, r_plot * r_b) # ------- # circle fill(1, 0, 0) # get the point on a circle x_c, y_c = cos(angle), sin(angle) # draw the point and a rect for the bar chart oval(x_c * r - dia/2, c_plot_y + y_c * r - dia/2, dia, dia) rect((angle/(pi/2)) * r - dia_/2, r_plot_y, dia_, r_plot) fill(.3) if i % 10 == 0: x_p, y_p = r * f, margin #* 1.5 rect(x_p - .25, y_p, .5, 30) text('%d°' % (f * 90), (x_p-2, y_p * 1.5)) print (max_off) text('%.6f' % max_off, (-50, max_off * r_plot - r_plot + margin - 2)) text('%.6f' % 1, (-50, margin - 2))The maybe more interesting peculiarity of bezier curves is the difference between time and distance. We can compare the bezier distance at factor f (0-1) to the circle if we use the same factor to get the appropriate fraction of 90 degrees.
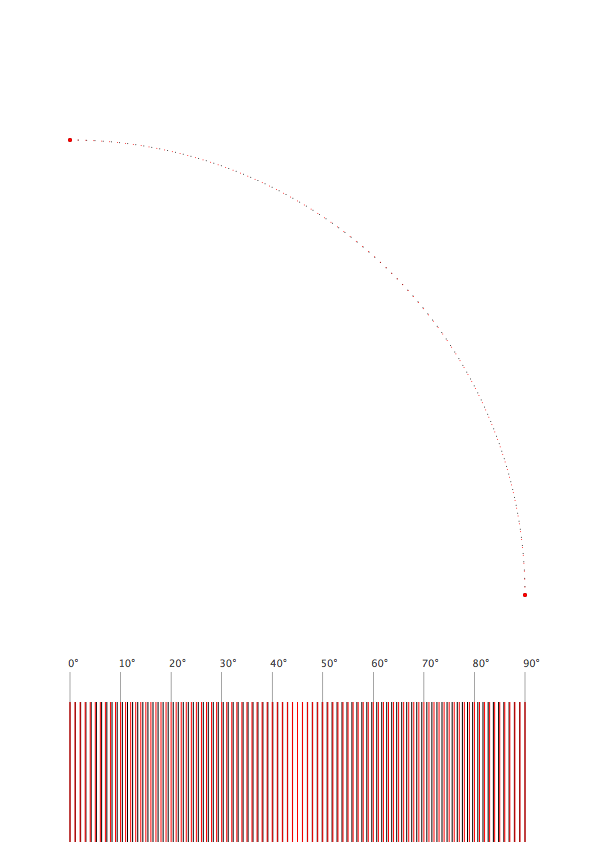
Code
# ------------------- # settings pw, ph = 595, 842 #A4 margin = 70 tang = 4*(sqrt(2)-1)/3 r = pw - 2 * margin density = 90 # amount of points dia_ = 1 # diameter to draw the points r_plot = 100000 # this is a magnifying factor to make the tiny difference visible. r_plot_y = margin - r_plot #radius plotting c_plot_y = ph - 3 * margin - r # circle plotting # ------------------- # functions def get_bezier_p(p1, t1, t2, p2, t): ''' get the point on a bezier curve at t (should be between 0 and 1) ''' x = (1 - t)**3 * p1[0] + 3*(1 - t)**2 * t * t1[0] + 3*(1 - t)* t**2 * t2[0] + t**3 * p2[0] y = (1 - t)**3 * p1[1] + 3*(1 - t)**2 * t * t1[1] + 3*(1 - t)* t**2 * t2[1] + t**3 * p2[1] return x, y def get_dist(p1, p2): ''' returns the distance between two points (x, y)''' return sqrt((p2[0]-p1[0])**2 + (p2[1]-p1[1])**2) # ------------------- # drawings newPage(pw, ph) fill(1) rect(0, 0, pw, ph) translate(margin, margin) # draw the tangent points rect(r - dia_, c_plot_y + tang*r - dia_, dia_*2, dia_*2) rect(tang*r -dia_, c_plot_y + r - dia_, dia_*2, dia_*2) for i in range(density+1): # ------- # bezier # calculate the factor f f = i/density fill(0) if i == 0 or i == (density): dia = dia_ * 4 else: dia = dia_ # get the coordinates for the point at factor f x_b, y_b = get_bezier_p( (1, 0), (1, tang), (tang, 1), (0, 1), f ) # get the distance of the point from the center at (0, 0) r_b = get_dist((0, 0), (x_b, y_b)) # get the angle of the point angle = atan2(y_b, x_b) # draw the point and a rect for the bar chart oval(x_b * r - dia/2, c_plot_y + y_b * r - dia/2, dia, dia) rect((angle/(pi/2)) * r - dia_/2, r_plot_y, dia_, r_plot) # ------- # circle fill(1, 0, 0) # get the point on a circle x_c, y_c = cos( pi/2*f ), sin( pi/2*f ) # draw the point and a rect for the bar chart oval(x_c * r - dia/2, c_plot_y + y_c * r - dia/2, dia, dia) rect(f * r - dia_/2, r_plot_y, dia_, r_plot) fill(.3) if i % 10 == 0: x_p, y_p = r * f, margin #* 1.5 rect(x_p - .25, y_p, .5, 30) text('%d°' % (f * 90), (x_p-2, y_p * 1.5))
Latest posts made by jo
-
RE: Help with code & combining ideaposted in Code snippets
@frederik ah, that is super helpful!
How did I miss this great feature?
Thanks again -
RE: Help with code & combining ideaposted in Code snippets
@frederik
Sad that the forum will be discontinued, so thanks a lot for keeping it up for so long and leaving it in read only mode.I will still try to post one more question, since I am frequently wondering how to do that in a clever way.
Like in the example above I usually try to have all the settings (like the definition of the page dimensions) in one place and before doing any drawing.
But I can only get the width if there is already a page (or it will be the default 1000).
How could I get the dimenations of eg an A3 page without callingnewPage('A3')?Again thanks for drawbot and the forum. See you on discord!
-
RE: Help with code & combining ideaposted in Code snippets
aah, untested last minute changes. I changed the variable names to something more reasonable but forgot one instance.
cell_hshould belabel_h.PW, PH = 842, 1190 # A3 page width and height page_margin = 40 # the margin for the whole page amount = 50 # how many labels to draw in total per_page = 10 # how many labels per page gap = 10 # the gap between the labels # the next line calculates the heigth for the label label_h = (PH - ((per_page-1)*gap) - 2 * page_margin ) / per_page for i in range(amount): if i % per_page == 0: newPage(PW, PH) y = PH - page_margin - label_h rect(page_margin, y, width() - 2*page_margin, label_h) y -= label_h + gap -
RE: Help with code & combining ideaposted in Code snippets
you could new make an A3 page with
newPage('A3')
and then draw several of the textboxes on that page. basically take thenewPageout of the loop and instead change the position of each new label.PW, PH = 842, 1190 # A3 page width and height page_margin = 40 # the margin for the whole page amount = 50 # how many labels to draw in total per_page = 10 # how many labels per page gap = 10 # the gap between the labels # the next line calculates the heigth for the label label_h = (PH - ((per_page-1)*gap) - 2 * page_margin ) / per_page for i in range(amount): if i % per_page == 0: newPage(PW, PH) y = PH - page_margin - cell_h rect(page_margin, y, width() - 2*page_margin, label_h) y -= label_h + gap -
RE: Defining lineHeight and first baseline: status?posted in Bugs
thanks for clarifying.
one thing that made me wonder when reading the unconventional UPM of 550: might this be related to this bug: https://github.com/typemytype/drawbot/issues/555#issuecomment-1948050444.as @monomonnik suggests I also tried a simpler script with Mutator Sans and I think this does what you expect?
txt = 'lestextessociologiques'.upper() fnt = 'MutatorSans.ttf' fnt_s = 24 lh = 32 lh_shift = -3 rows = 11 newPage('A4') txt_l = len(txt) fstr = FormattedString(fontSize = fnt_s, font = fnt) for r_i in range(rows): for t_i in range(txt_l): fstr.append(txt[(t_i + r_i)%txt_l], font = fnt, fontSize = fnt_s, lineHeight = lh, fontVariations={'wght': 1000/rows * r_i, 'wdth': 1000/txt_l*t_i}) fstr.append('\n') lh += lh_shift if r_i < rows/2 else -lh_shift text(fstr, (20, height() - 100))
otherwise just using a
text()for each line might me a way?txt = 'lestextessociologiques'.upper() fnt = '/Users/jo/Desktop/MutatorSans.ttf' fnt_s = 24 lh = 50 lh_shift = -3 rows = 11 newPage('A4') txt_l = len(txt) y = height() - 100 for r_i in range(rows): fstr = FormattedString(fontSize = fnt_s, font = fnt) for t_i in range(txt_l): fstr.append(txt[(t_i + r_i)%txt_l], font = fnt, fontSize = fnt_s, fontVariations={'wght': 1000/rows * r_i, 'wdth': 1000/txt_l*t_i}) text(fstr, (10, y)) lh += lh_shift if r_i < rows/2 else -lh_shift y -= lh -
RE: Defining lineHeight and first baseline: status?posted in Bugs
not sure I understand your question correctly.
my assumption is you want to specify a position for the first baseline and have the textbox draw the text so the first line is at that given position no matter the lineheight or font size?
the following script should do that. I tested a few fonts, fontSizes and lineHeights.# ----------------------------------- # S E T T I N G S fnt = 'Helvetica' fnt_s = 16 # the fontsize lh = fnt_s * 1.6 # the lineheight txt = 'Testing the position of the baseline and the setting of the line height in drawBot. '*30 tbx_x = 100 # x position of the textbox frst_bl_y = 657 # the exact position of the first baseline within the textbox tbx_w = 350 # textbox width tbx_h = 400 # textbox heigth # -------------- # F U N C T I O N S def calc_baseline_offset(fnt, fnt_s, lh): '''calculates the position of the first baseline of a placeholder textbox and returns the distance from the top edge of the textbox''' fstr = FormattedString('Hm', font = fnt, fontSize = fnt_s, lineHeight = lh) temp_first_baseline = textBoxBaselines(fstr, (0, 0, fnt_s * 3, fnt_s * lh))[0][1] return temp_first_baseline - (fnt_s * lh) # ----------------------------------- # D R A W I N G S newPage('A4') fstr = FormattedString(txt, font = fnt, fontSize = fnt_s, lineHeight = lh) rect(tbx_x - 20, frst_bl_y, tbx_w + 40, -1) # drawing the first baseline y_shift = calc_baseline_offset(fnt, fnt_s, lh) tbx_y = frst_bl_y - tbx_h - y_shift # the y position for the textbox so that the first baseline stays at the given value fill(1, 0, 0, .1) rect(tbx_x, tbx_y, tbx_w, tbx_h) textBox(fstr, (tbx_x, tbx_y, tbx_w, tbx_h)) # drawing all the baselines for x, y in textBoxBaselines(fstr, (tbx_x, tbx_y, tbx_w, tbx_h)): rect(tbx_x, y, tbx_w, -1)
-
RE: QRCodeGenerator(size, message)posted in General Discussion
I ran into the same issue a few weeks ago and @frederik actually posted another solution in the other QR code thread:
going through the pixels and checking the lightness/brightness:
https://forum.drawbot.com/topic/397/qr-code-with-type?_=1681732270808Using a module has the nice advantage of checking the size of the QR code after generating it.
-
RE: trim box in pdfsposted in Feature Requests
@monomonnik thanks, yes that is how i 'solved' it but when doing that with several files it gets a bit tedious. not a big deal but maybe it is can be easily stored during the export in drawbot.
-
trim box in pdfsposted in Feature Requests
hello,
Whenever I place a pdf in InDesign I get the error message:
'Cannot crop to trim box. Either the trim box is not defined, or is empty'.Is there a way to include a trimbox in the pdfs saved from Drawbot or is this InDesign related?
thanks j -
RE: when to apply paragraphBottomSpacingposted in Feature Requests
oké
I had some small hope but thanks for testing and clarifying!not very elegant but kind of working:
txt = 'Some Text\nwith new lines\rIs a return\na new line\ror a new paragraph?' paras = [[l + '\n' for l in p.split('\n')] for p in txt.split('\r')] newPage(150, 150) fstr = FormattedString() for para in paras: for l in para: extra_space = 5 if l == para[-1] else 0 fstr.append(l, paragraphBottomSpacing = extra_space) text(fstr, (20, 110))