Animated Müller-Lyer illusion
-
nautil.us has a nice blogpost of optical illusions. I could not resist the attempt to build one of them in drawbot.
pw = ph = 400 # define variables to set width and height of the canvas cols = 14 # define how many columns there should be rows = 4 # define how many rows there should be pages = 30 # define how many frames the gif should have. more pages mean slower movement angle_diff = 2 * pi/pages # we want the loop to make one full circle. 2 times pi is 360 degrees. Divided by the amount of pages this gives us the angle difference between pages. gap = pw/(cols+1) # calculate the gap between the lines. l = (ph - 2 * gap)/rows # calculate the length of the line. for p in range(pages): newPage(pw, ph) translate(gap, gap) fill(None) strokeWidth(2) for x in range(cols): y_off = cos( 3 * pi * x/cols + angle_diff * p ) * gap/2 # calculate how high or low the arrowhead should be for y in range(rows+1): stroke(1,0 ,0) if y % 2 == 0 else stroke(0, 0, 1) if y < rows: line((x*gap, y*l), (x*gap, y*l+l)) stroke(0) y_off *= -1 # switch to change direction line( (x*gap, y*l), (x*gap - gap/2, y*l - y_off) ) line( (x*gap, y*l), (x*gap + gap/2, y*l - y_off) ) # saveImage('~/Desktop/opti_illu.gif')this should generate something like this:
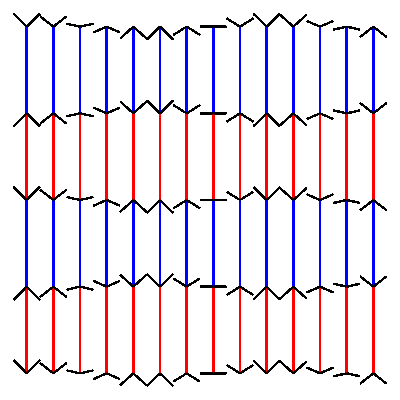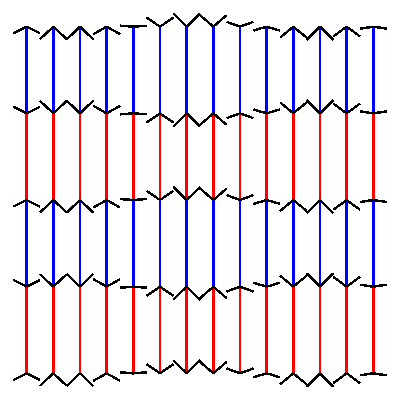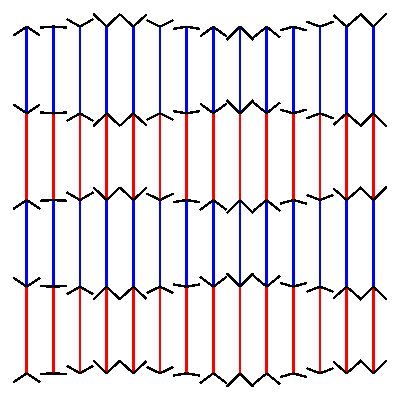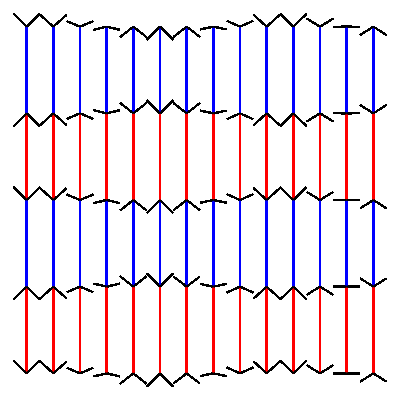
-
Here's code for another, the 'intertwining illusion'.
canvas = 500 nFrames = 60 #240 size = canvas/36 num1 = 60 num2 = 44 num3 = 30 num4 = 14 r = 15 def mod(rot): m = BezierPath() m.rect(-size/2, -size/2, size, size) m.closePath() m.rotate(rot) drawPath(m) for n in range(nFrames): newPage(canvas, canvas) frameDuration(1/30) fill(.5) rect(0, 0, canvas, canvas) strokeWidth(3) translate(canvas/2, canvas/2) save() for i in range(num1): if i % 2 == 0: stroke(1) else: stroke(.15) save() translate(.8 * canvas/2, 0) mod(r * (sin(2 * pi * n/nFrames))) restore() rotate(360/num1) restore() save() for j in range(num2): if j % 2 == 0: stroke(1) else: stroke(.15) save() translate(.6 * canvas/2, 0) mod(-r * (sin(2 * pi * n/nFrames))) restore() rotate(360/num2) restore() save() for k in range(num3): if k % 2 == 0: stroke(1) else: stroke(.15) save() translate(.4 * canvas/2, 0) mod(r * (sin(2 * pi * n/nFrames))) restore() rotate(360/num3) restore() save() for l in range(num4): if l % 2 == 0: stroke(1) else: stroke(.15) save() translate(.2 * canvas/2, 0) mod(-r * (sin(2 * pi * n/nFrames))) restore() rotate(360/num4) restore() saveImage('~/Desktop/opart_intertwine.gif')The more frames, the more subtle the shift.

-
And here's yet another—I forget the name of the illusion just now.
canvas = 500 #750 number = 15 shape = canvas/15 small = shape/2 offset = shape nFrames = 90 #240 r = 5 def semi(pos, rot): s = BezierPath() if pos == 'top': s.arc((0, 0), shape/2, 0, 180, False) elif pos == 'bottom': s.arc((0, 0), shape/2, 0, 180, True) s.closePath() s.rotate(rot) drawPath(s) for n in range(nFrames): newPage(canvas, canvas) frameDuration(1/30) fill(.85) rect(0, 0, canvas, canvas) translate(canvas/2, canvas/2) save() translate(-(number - 1) * offset/2, (number - 1) * offset/2) fill(.2) for i in range(number): save() translate(0, i * -offset) if (i % 2) == 0: v = 1 elif (i % 2) == 1: v = -1 for j in range(number): save() translate(j * offset, 0) if (j % 2) == 0: semi('top', r * (sin((2 * pi) * (n/nFrames))) * v) elif (j % 2) == 1: semi('bottom', r * (sin((2 * pi) * (n/nFrames))) * v) restore() restore() restore() translate(0, (number - 1) * offset/2) for i in range(number): save() translate(0, i * -offset) if (i % 2) == 0: fill(1) oval((cos((2 * pi) * (n/nFrames)) * canvas/2) - small/2, 0, small, small) elif (i % 2) == 1: fill(1) oval((cos((2 * pi) * (n/nFrames)) * -canvas/2) - small/2, 0, small, small) restore() saveImage('~/Desktop/op_semi_lines.gif')With both sketches, a larger canvas and more frames (240+) makes for a better effect.

-
@mauricemeilleur cool! thanks for sharing
the 4 'rings' could also be made inside a for loop, the variable is in the translate factor of the size of the canvas

-
True—both these sketches are quickies from last year, when I was still learning my way around the code.
-
nice, ones!
here is one more:grid = 12 page_s = 600 frames = 48 tile_s = page_s/grid rhythm = [1, 0, 0, 1, 0, 1, 1, 0] def cross(pos, s): x, y = pos polygon((x - s/2, y), (x - s/2 + s/8, y - s/8), (x - s/8, y - s/8), (x - s/8, y - s/2 + s/8), (x, y - s/2), (x + s/8, y - s/2 + s/8), (x + s/8, y - s/8), (x + s/2 - s/8, y - s/8), (x + s/2, y), (x + s/2 - s/8, y + s/8), (x + s/8, y + s/8), (x + s/8, y + s/2 - s/8), (x, y + s/2), (x - s/8, y + s/2 - s/8), (x - s/8, y + s/8), (x - s/2 + s/8, y + s/8) ) for f in range(frames): newPage(page_s, page_s) frameDuration(.1) # linear alpha = f / frames if f < (frames) else 2 - (f / frames) # sinus wave alpha = .5 + .5 * sin(f/frames * 2 * pi) for y in range(grid): for x in range(grid): fill(.8) if (x+y) % 2 == 0 else fill(.7) rect(x * tile_s, y * tile_s, tile_s, tile_s) shift = (x + y) % len(rhythm) fill(1, alpha) if rhythm[ shift ] else fill(.5, alpha) cross((x * tile_s, y * tile_s), tile_s/3 ) # saveImage('wavy_checkerboard.gif')
-
ok, one more.
very similar to the previous one.page_s = 500 cell_amount = 12 rhythm = [1, 0, 0, 1, 0, 1, 1, 0] cell_s = page_s / cell_amount corner_s = cell_s/4 newPage(page_s, page_s) translate(-cell_s/2, -cell_s/2) def lozenge(pos, s): x, y = pos polygon((x, y), (x + s/2, y + s/2), (x + s, y), (x + s/2, y - s/2)) for x in range(cell_amount+1): for y in range(cell_amount+1): pos_x, pos_y = x * cell_s, y * cell_s fill(0.5) if (x+y) % 2 == 0 else fill(1) rect(pos_x, pos_y, cell_s, cell_s) fill(1) lozenge((pos_x - corner_s, pos_y), corner_s*2) fill(0) shift = (x + y) % len(rhythm) if rhythm[ shift ]: lozenge((pos_x - corner_s, pos_y), corner_s) lozenge((pos_x, pos_y), corner_s) else: lozenge((pos_x - corner_s/2, pos_y + corner_s/2), corner_s) lozenge((pos_x - corner_s/2, pos_y - corner_s/2), corner_s)