arcTo documentation?
-
So, there have been two things that have bugged me since I started working with DrawBot a couple years ago. One is very simple and has to do with the documentation for arcTo().
canvas = 500 size = canvas/2 newPage(canvas, canvas) fill(1) rect(0, 0, canvas, canvas) translate(canvas/2, canvas/2) stroke(0) p = BezierPath() p.moveTo((0, size/2)) p.lineTo((0, 0)) p.lineTo((size/2, 0)) print(p.points) drawPath(p)
My list of points is:
[(0.0, 125.0), (0.0, 0.0), (125.0, 0.0)]So let's say I want to close that path to make a quarter-circle. The documentation for arcTo() says:
arcTo(pt1, pt2, radius)
Arc from one point to another point with a given radius.Well, I know the two points I want to connect: (0, size/2) and (size/2, 0). But what does 'radius' tell me in this context? It's obvious for the arc() method, because there you specify a center point with the radius. If I just enter my points and set radius to size/2:
… p = BezierPath() p.moveTo((0, size/2)) p.lineTo((0, 0)) p.lineTo((size/2, 0)) p.arcTo((size/2, 0), (0, size/2), size/2) …I get a shape visibly unchanged:

and this list of points:
[(0.0, 125.0), (0.0, 0.0), (125.0, 0.0), (125.0, 0.0), (125.0, 0.0), (125.0, 0.0), (125.0, 0.0), (125.0, 0.0), (125.0, 0.0), (125.0, 0.0)]If I use (size/2, size/2) as my first point:
… p = BezierPath() p.moveTo((0, size/2)) p.lineTo((0, 0)) p.lineTo((size/2, 0)) p.arcTo((size/2, size/2), (0, size/2), size/2) …I get the shape I want:
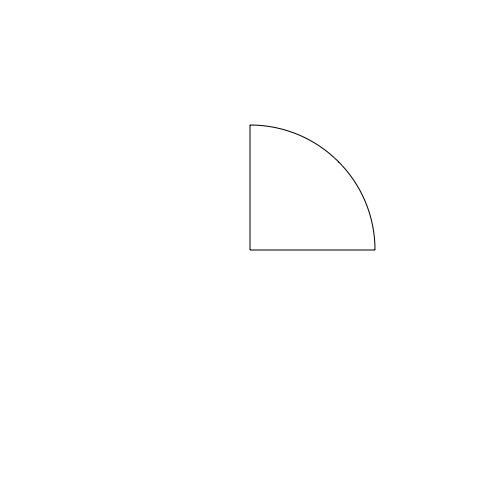
and this list of points:
[(0.0, 125.0), (0.0, 0.0), (125.0, 0.0), (125.0, -2.0767666935733048e-14), (125.0, 69.03559372884915), (69.03559372884918, 124.99999999999999), (7.654042494670958e-15, 124.99999999999999), (7.654042494670958e-15, 124.99999999999999), (-4.785710873658687e-14, 124.99999999999999), (-4.785710873658687e-14, 124.99999999999999)]So does this mean I'm not drawing an arc between xy1 and xy2, but instead defining an off-curve point with xy1 and an on-curve point with xy2? If so, what is radius telling me? Because if I change it to (size), here's the shape I get:
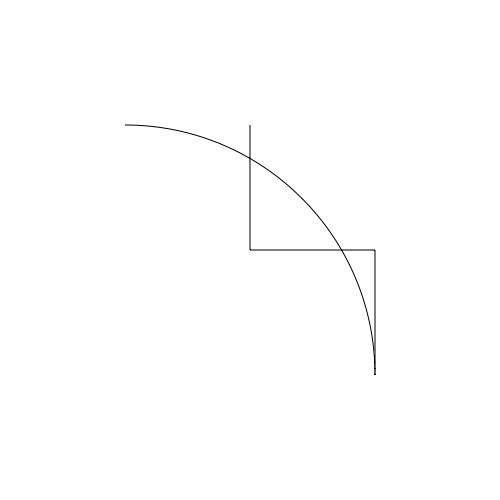
and my list of points:
[(0.0, 125.0), (0.0, 0.0), (125.0, 0.0), (125.0, -125.00000000000004), (125.0, 13.071187457698286), (13.071187457698343, 124.99999999999994), (-124.99999999999999, 124.99999999999996), (-124.99999999999999, 124.99999999999996), (-125.0000000000001, 124.99999999999996), (-125.0000000000001, 124.99999999999996)]I have a feeling that learning the answer to what's going on here will suggest the answer to the other thing that's been bugging me, which is the syntax for defining curves with points—how do I know/specify which ones are the on-curve and off-curve points?
Thanks in advance to anyone who can help. I suspect this is something pretty basic which people who get exposed to DrawBot or RoboFont in a different way than I did understand implicitly, so I apologize if my questions sound elementary.
-
And since I'm asking: Looking at these lists of points, how do I know which ones are what in an application like Illustrator we'd call the 'corner points', where the 'handles' = off-curve points are not collinear with the 'anchors = on-curve points between them? Again, sorry in advance if these are really elementary questions …
-
path.arcTo(pt1, pt2, radius)draws a line between the current point (fe a previously set moveTo) topt1and arcs topt2with a given radius:path = BezierPath() path.moveTo((100, 100)) path.arcTo((150, 100), (200, 200), 30) fill(None) stroke(0) drawPath(path)there are different ways of looking at a BezierPath object:
- as flat list of points:
path.points - as a list of contours:
for contour in path: - as a nested list of contours with segments:
for contour in path: for segment in contour: # line # on curve # curve # off curve, off curve, on curve print(segment)
- as flat list of points:
-
I've marked the points in the curve to try to make sense of its behavior: green for the starting point, red for the others.
canvas = 300 start = (100, 100) pt1 = (200, 100) pt2 = (200, 200) radius = 100 newPage(canvas, canvas) fill(1) rect(0, 0, canvas, canvas) path = BezierPath() path.moveTo(start) path.arcTo(pt1, pt2, radius) fill(None) stroke(0) drawPath(path) stroke(None) start = list(start) pt1 = list(pt1) pt2 = list(pt2) fill(0, 1, 0) oval(start[0] - 1, start[1] - 1, 2, 2) fill(1, 0, 0) oval(pt1[0] - 1, pt1[1] - 1, 2, 2) oval(pt2[0] - 1, pt2[1] - 1, 2, 2) print(path.points)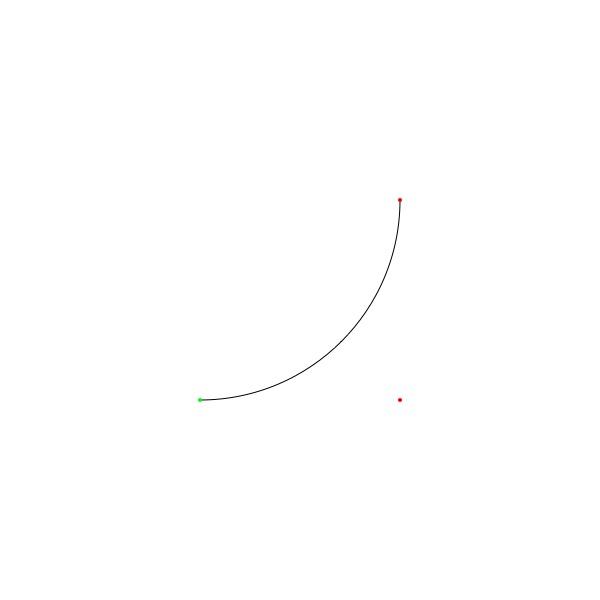
So that first defined point in arcTo() feels like an off-curve or control point, right? But then pt2 must be more than just the point to which the arc curves, because if I change radius to 400 I get this:
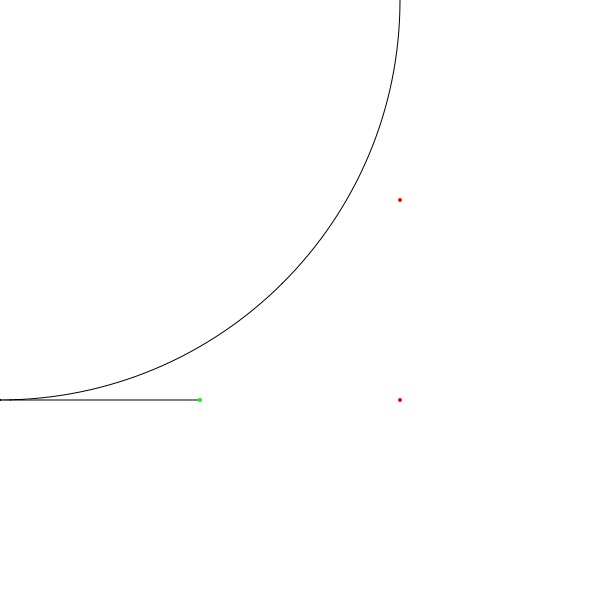
and if I change pt1 to (400, 300) I get this:

I'm just having a hard time telling a story about what these points are doing that makes sense to me …
-
I understand the confusion

a much better explanation:
The created arc is defined by a circle inscribed inside the angle specified by three points: the current point, the fromPoint parameter, and the toPoint parameter (in that order). The arc itself lies on the perimeter of the circle, whose radius is specified by the radius parameter. The arc is drawn between the two points of the circle that are tangent to the two legs of the angle.
The arc usually does not contain the points in the fromPoint and toPoint parameters. If the starting point of the arc does not coincide with the current point, a line is drawn between the two points. The starting point of the arc lies on the line defined by the current point and the fromPoint parameter.I will adjust the drawBot documentation
-
now it makes sense!

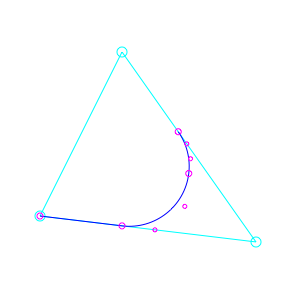
def drawPt(pos, r=5): x, y = pos oval(x-r, y-r, r*2, r*2) pt0 = 40, 84 pt1 = 256, 58 pt2 = 122, 248 size(300, 300) fill(None) path = BezierPath() path.moveTo(pt0) path.arcTo(pt1, pt2, 60) stroke(0, 1, 1) polygon(pt0, pt1, pt2) for pt in [pt0, pt1, pt2]: drawPt(pt) stroke(0, 0, 1) drawPath(path) stroke(1, 0, 1) for pt in path.onCurvePoints: drawPt(pt, r=3) for pt in path.offCurvePoints: drawPt(pt, r=2)
-
super nice drawing! thanks @gferreira
-