Possible solution to Just's puzzle?

erik

https://twitter.com/justvanrossum/status/952108619159531520

# a possible solution to Just's puzzle?
size(1000,1000)
fill(0)
dia = 864
rect(0,0,width(),height())
for d in range(1, dia):
    d = dia-d
    fill((dia-d)/dia)
    oval(350-.5*d, 750-.5*d, d, d)
    oval(650-.5*d, 250-.5*d, d, d)

justvanrossum

@erik Very close. Ready for spoilers?

JeremieHornus

Something like that ?

fill(math.sqrt((dia-d)/dia))

justvanrossum

@jeremiehornus Oh, that looks lovely! But no, what I did was way stupider in some way...

dyb

A silly question but do we see the circles as bubbles melting together simply because they are put on the canvas alternately?

I guess you could also use the "Lighten" blending mode and just fill the circles with gradients.

JeremieHornus

@justvanrossum building on @erik solution:

import random, math, noise

w = 500
h = 500

dia = 100
rows = 5
cols = 5
ovals = []

frames = 30

for x in range(1, rows):
    for y in range(1, cols):
        ovals.append((x*(w/rows), y*h/cols, 1+.5*random.random()))

for f in range(frames):
    newPage(w, h)
    frameDuration(1/20)
    fill(0)
    rect(0,0,width(),height())
    n = f/frames
    for d in range(1, dia):
        d = dia-d
        fill(.9*math.sqrt((dia-d)/dia))
        
        for i, (x, y, g) in enumerate(ovals):
            m = noise.pnoise3(.1*x/w, .1*y/h, i+ .5*math.sin(2*math.pi*(f/frames)))
            oval(20*m + x-.5*d*g*(1+m), 20*m +  y-.5*d*g*(1+m), d*g*(1+m), d*g*(1+m))

saveImage("Just2.mp4")

justvanrossum

How about a radialGradient()?

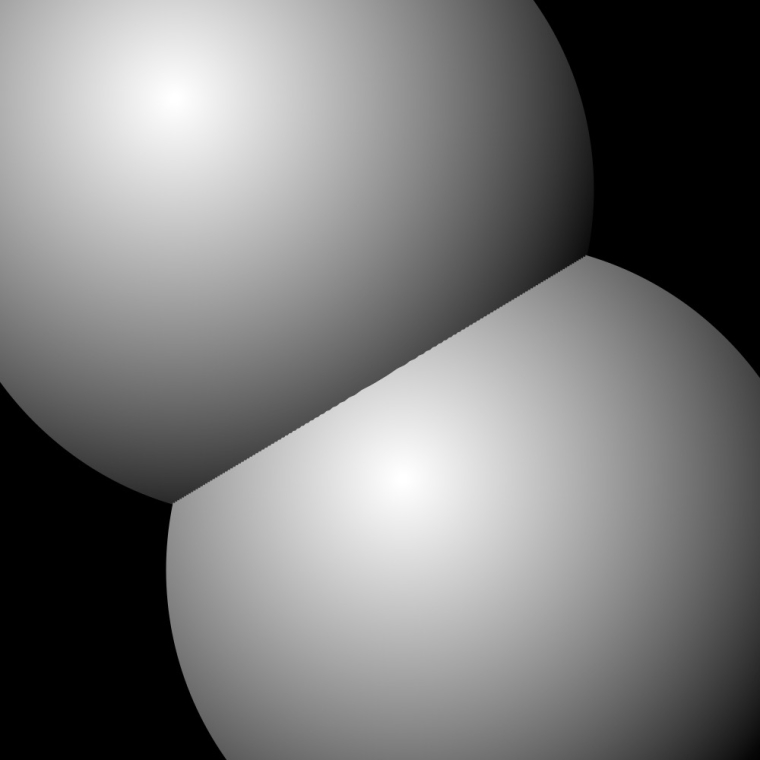
size(1000, 1000)
fill(0)
dia = 864
offset = 120
rect(0, 0, width(), height())
for d in range(1, dia, 5):
    d = dia-d
    radialGradient((350-offset, 750+offset),
            (350-offset, 750+offset), [(1,), (0,)],
            startRadius=5, endRadius=0.7*dia)
    oval(350-.5*d, 750-.5*d, d, d)
    radialGradient((650-offset, 250+offset),
            (650-offset, 250+offset), [(1,), (0,)],
            startRadius=5, endRadius=0.7*dia)
    oval(650-.5*d, 250-.5*d, d, d)

justvanrossum

But I must say I really love the foggy effect of @JeremieHornus's solution.

dyb

An example with blendMode("lighten") and radialGradient() building on @justvanrossum example.

size(1000, 1000)
fill(0)
dia = 864
offset = 120
rect(0, 0, width(), height())
d = 1200

blendMode("lighten")

radialGradient((350-offset, 750+offset),
        (350-offset, 750+offset), [(1,), (0,)],
        startRadius=5, endRadius=0.7*dia)
oval(350-.5*d, 750-.5*d, d, d)

radialGradient((650-offset, 250+offset),
        (650-offset, 250+offset), [(1,), (0,)],
        startRadius=5, endRadius=0.35*dia)
oval(650-.5*d, 250-.5*d, d, d)