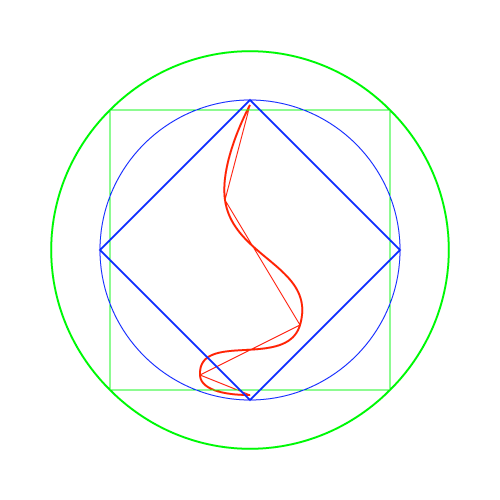
Round Corners
-
The code responsible for the rounding of the paths in a small animation I made.
DEBUG = False # A path has points. # A point has only an anchor [(x,y)], or has an anchor and in and out point [(x,y), (x,y), (x,y)]. # To close a path, repeat the first point at the last position. jagged_line =[[(500,210)], [(400,250)], [(600,350)], [(450,600)], [(500,790)]] rectangle =[[(220,220)], [(780,220)], [(780,780)], [(220,780)], [(220,220)]] circle = [[(500.0, 800.0), (335.0, 800.0), (665.0, 800.0)], [(800.0, 500.0), (800.0, 665.0), (800.0, 335.0)], [(500.0, 200.0), (665.0, 200.0), (335.0, 200.0)], [(200.0, 500.0), (200.0, 335.0), (200.0, 665.0)], [(500.0, 800.0), (335.0, 800.0), (665.0, 800.0)]] def draw(path): bez = BezierPath() bez.moveTo(path[0][0]) for i in range(1, len(path)): p0 = path[i-1] p1 = path[i] if len(p0) == 1 and len(p1) == 1: # straight line between points bez.lineTo(p1[0]) elif len(p0) == 3 and len(p1) == 1: # from curve point to straight point bez.curveTo(p0[2], p1[0], p1[0]) elif len(p0) == 1 and len(p1) == 3: # from straight point to curve point bez.curveTo(p0[0], p1[1], p1[0]) elif len(p0) == 3 and len(p1) == 3: # curve point on both sides bez.curveTo(p0[2], p1[1], p1[0]) if path[-1] == path[0]: bez.closePath() drawPath(bez) def round_corners(path, roundness): if len(path) > 2: new_path = [] new_path.append(path[0]) new_path.append(path[1]) for i in range(1, len(path) - 1): p1 = new_path[i - 1] p2 = path[i] p3 = path[i + 1] p1, p2, p3 = round_segment(p1, p2, p3, roundness) new_path[i - 1] = p1 new_path[i] = p2 new_path.append(p3) # If the path is closed, we need (the handle of) the first point if path[-1] == path[0]: p1 = new_path[-2] p2 = path[0] p3 = new_path[1] p1, p2, p3 = round_segment(p1, p2, p3, roundness) new_path[-2] = p1 new_path[-1] = p2 new_path[0] = p2 return new_path else: return path def round_segment(p1, p2, p3, roundness): if roundable(p1, p2, p3): p2_in, p2_out = create_handles(p1[0], p2[0], p3[0], roundness) p2 = [p2[0], p2_in, p2_out] return p1, p2, p3 def roundable(p1, p2, p3): # If two of the three points are in the same spot, # we can’t calculate a curve between two points. p1_anchor = p1[0] p2_anchor = p2[0] p3_anchor = p3[0] d12 = distance_between(p1_anchor, p2_anchor) d23 = distance_between(p2_anchor, p3_anchor) if d12 == 0 or d23 == 0: return False else: return True def create_handles(A, B, C, smoothness): # A is the point before point B # B is the point to create the handles for # C is the point after point B d_AB = distance_between(A, B) d_BC = distance_between(B, C) # Create an isosceles triangle A, B, p4 based on triangle A, B, C. # Side B, p4 is the same length as side A, B. # Side B, p4 has the same direction as side B, C p4_x = ((C[0] - B[0]) * (d_AB / d_BC)) + B[0] p4_y = ((C[1] - B[1]) * (d_AB / d_BC)) + B[1] p4 = (p4_x, p4_y) if DEBUG: draw_handle(B, p4) # Calculate a point p5 on the base of the isosceles triangle, # exactly in between A and B. p5_x = A[0] + ((p4[0] - A[0]) / 2) p5_y = A[1] + ((p4[1] - A[1]) / 2) p5 = (p5_x, p5_y) if DEBUG: draw_point(p5, 10) draw_line(A, p4) # The line from the top of the isosceles triangle B to # the point p5 on the base of that triangle # divides the corner p1, p2, p3 in two equal parts if DEBUG: draw_line(B, p5) # Direction of the handles is perpendicular vx = p5[0] - B[0] vy = p5[1] - B[1] handle_vx = 0 handle_vy = 0 if vx == 0 and vy == 0: # The three points are on one line, so there will never be a curve. pass elif vx == 0: # prevent a possible division by 0 handle_vx = 1 handle_vy = 0 elif vy == 0: # prevent a possible division by 0 handle_vx = 0 handle_vy = 1 elif abs(vx) < abs(vy): handle_vx = 1 handle_vy = vx / vy else: handle_vx = vy / vx handle_vy = 1 # Define handles handle_a = (B[0] + handle_vx, B[1] - handle_vy) handle_b = (B[0] - handle_vx, B[1] + handle_vy) # The handle closest to point A will be the incoming handle of point B d_ha_A = distance_between(A, handle_a) d_hb_A = distance_between(A, handle_b) # I have to make this better. Also, where’s that 0.8 coming from? What was I thinking? incoming_handle_lenght = d_AB * smoothness outgoing_handle_length = d_BC * smoothness total_handle_length = incoming_handle_lenght + outgoing_handle_length max_handle_length = 0.8 * total_handle_length if incoming_handle_lenght > max_handle_length: outgoing_handle_length += incoming_handle_lenght - max_handle_length incoming_handle_lenght = max_handle_length if outgoing_handle_length > max_handle_length: incoming_handle_lenght += outgoing_handle_length - max_handle_length outgoing_handle_length = max_handle_length # finally, the in and out points if d_ha_A < d_hb_A: B_incoming = (B[0] + handle_vx * incoming_handle_lenght, B[1] - handle_vy * incoming_handle_lenght) B_outgoing = (B[0] - handle_vx * outgoing_handle_length, B[1] + handle_vy * outgoing_handle_length) else: B_incoming = (B[0] - handle_vx * incoming_handle_lenght, B[1] + handle_vy * incoming_handle_lenght) B_outgoing = (B[0] + handle_vx * outgoing_handle_length, B[1] - handle_vy * outgoing_handle_length) if DEBUG: draw_point(B_incoming, 6) draw_point(B_outgoing, 6) draw_line(B, B_incoming) draw_line(B, B_outgoing) draw_line(A, B) return B_incoming, B_outgoing def distance_between(p1, p2): dx = p2[0] - p1[0] dy = p2[1] - p1[1] return pow((dx * dx + dy * dy), 0.5) def draw_point(point, size): with savedState(): fill(0, 0.7, 1) stroke(None) oval(point[0] - 0.5 * size, point[1] - 0.5 * size, size, size) def draw_line(a, b): with savedState(): fill(None) strokeWidth(1) stroke(0, 0.7, 1) line((100, 100), (900, 900)) line(a, b) def draw_handle(p, h): draw_point(p, 9) draw_line(p, h) fill(None) # Drawing the original shape and the rounded shape, slightly thicker. stroke(1, 0, 0) strokeWidth(2) draw(jagged_line) rounded_line = round_corners(jagged_line, 0.4) strokeWidth(4) draw(rounded_line) # A rounding of 0.28 seems to get me as close to a circle as I can get. stroke(0, 1, 0) strokeWidth(2) draw(rectangle) rounded_rectangle = round_corners(rectangle, 0.28) strokeWidth(4) draw(rounded_rectangle) # Rounding an oval by zero results in a rhombus. stroke(0, 0, 1) strokeWidth(2) draw(circle) rounded_circle = round_corners(circle, 0) strokeWidth(4) draw(rounded_circle)