Stroke alignment in shape
-
Hi! Is possible to set stroke alignment for oval and rects?
Maybe it oculd be handy to have this in a simple way that you can switch between 'center', 'inside' and 'outside'In this thread is a possible solution but for path https://forum.drawbot.com/topic/191/place-stroke-on-a-shape-s-contour-with-no-offset
Best
-
The solution in the tread you mention is a very nice solution

-
hello @guidoferreyra,
ovals and rects are also available as methods of
BezierPath, so you can use that same solution to draw the stroke inwards.to draw the stroke outwards, you can draw the shape with a doubled stroke first, and then draw it again on top using only the fill (so the internal half of the stroke is covered).
here’s an updated example showing all 3 “stroke modes”:
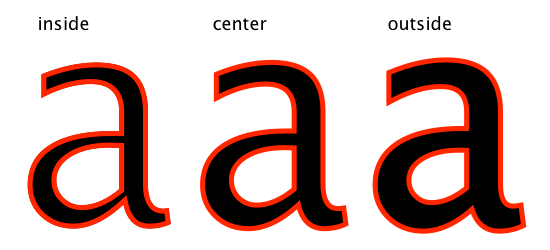
STROKEWIDTH = 20 B = BezierPath() B.text('a', (0, 0), fontSize=1200) # B.rect(0, 0, 500, 500) # B.oval(0, 0, 500, 500) size(2200, 1000) translate(50, 100) fontSize(72) for option in ['inside', 'center', 'outside']: text(option, (100, 780)) save() stroke(1, 0, 0) if option == 'inside': strokeWidth(STROKEWIDTH * 2) with savedState(): clipPath(B) drawPath(B) elif option == 'outside': strokeWidth(STROKEWIDTH * 2) drawPath(B) stroke(None) drawPath(B) else: strokeWidth(STROKEWIDTH) drawPath(B) restore() translate(700, 0)hope this helps! cheers
-
Great, thank you both!