A deeper bevel on lineJoin()?
-
Frederik, I'll take a look. I wonder if this and the feature requests I just made could be covered if I just learned more about how to use pens … I really don't want DrawBot to wind up like Illustrator, I swear!
-
I was working on a fold-font system a few years ago. it took some time to get the trigonometry right. but once that was solved the possibilities were endless ...
so the new alphabet could be rendered with different stroke weights


scaling in the x

or y direction

and there could be multi-liners

seems like i did not compensate for the stroke weight at the end of a stroke but the system could be used for any collection of xy-points

it is all a bit messy but let me know if you need some bits.
-
looks awesome!
-
@jo I'd love to see your code! Like I said, the way Crouwel used the corners was unrelated to the rules he used to construct the letterforms, so I could illustrate his structure without the beveled corners. But it would be nice in a presentation to show audiences the letters as he styled them.
-
@frederik Are all the import dependencies/paths in the outliner extension only going to make sense if I have RoboFont installed? Because I don't have RoboFont …
-
@mauricemeilleur I don’t know how Crouwel defined his rules. but to me the corner-rule seems like an integral part of the design.
I had a look at my code and tried to tidy the worst bits. some of the angle calculations seem very inefficient but ¯\(ツ)/¯ here it is:
EDIT 2018-05-28 changed the code to simplify some of the horrible trigonometry and there now is the
sq_capbool to have squared linecaps.# Draw a 'folded outline' between a set of points. # TO DO: There should be an error message when two dots are closer to each other and the weight. # There should be a warning if the folding is further than the next points. # There should be a warning for collinear points. import math # Just a bunch of points p01 = (894, 334) p02 = (808, 86) p03 = (274, 792) p04 = (481, 920) p05 = (583, 730) p06 = (85, 430) p07 = (318, 100) p08 = (870, 600) p09 = (720, 690) points = [p01, p02, p03, p04, p05, p06, p07, p08, p09] def get_dist(p1, p2): return sqrt( (p2[0] - p1[0] )**2 + (p2[1] - p1[1])**2 ) def calc_angle(p1, p2): return atan2((p2[1] - p1[1]), (p2[0] - p1[0])) def calc_delta(p1, p2, p3): ''' Returns the angle between three points. ''' return calc_angle(p2, p3) - calc_angle(p2, p1) def calc_offset(weight, p1, p2, p3): ''' Returns the x and y "offset" to be added to the points of the polygon. ''' halfWeight = weight/2 if p1 == p2: alpha = calc_angle(p1, p3) b = -sin(alpha) * halfWeight a = cos(alpha) * halfWeight elif p2 == p3: alpha = calc_angle(p1, p3) b = sin(alpha) * halfWeight a = -cos(alpha) * halfWeight else: alpha = calc_angle(p2, p3) delta = calc_delta(p1, p2, p3) xx = halfWeight / sin((delta - pi) / 2) delta_f = (2 * alpha - pi - delta ) / 2 a, b = xx * sin(delta_f), xx * cos(delta_f) return a, b def wrap_line(p1, p2, p3, p4, weight): ''' This draws a polygon around a line. Four points (x,y) and a weight parameter are required. The polygon will be drawn around the two middle points. The first and last points define the angles. ''' a, b = calc_offset(weight, p1, p2, p3) # extend first point x1b, y1b = p2[0] - b, p2[1] - a x1c, y1c = p2[0] + b, p2[1] + a # extend second point c, d = calc_offset(weight, p2, p3, p4) x2b, y2b = p3[0] - d, p3[1] - c x2c, y2c = p3[0] + d, p3[1] + c polygon((x1b, y1b), (x1c, y1c), (x2b, y2b), (x2c, y2c)) # -------------------------------------------------------------------- # The actual drawing fill(0, .4) weight = 180 sq_cap = True if len(points) == 1: rect(points[0][0] - weight/2, points[0][1] - weight/2, weight, weight) for i, point in enumerate(points[:-1]): # print (get_dist(point, points[i+1])) if len(points) == 2: wrap_line(points[i], points[i], points[i+1], points[i+1], weight) else: if i == 0: aaa = calc_angle(points[i], points[i+1]) if sq_cap: point = point[0] - weight/2 * cos(aaa), point[1] - weight/2 * sin(aaa) wrap_line(point, point, points[i+1], points[i+2], weight) elif i == len(points)-2: next_p = points[i+1] aaa = calc_angle(points[i], next_p) if sq_cap: next_p = next_p[0] + weight/2 * cos(aaa), next_p[1] + weight/2 * sin(aaa) wrap_line(points[i-1], points[i], next_p, next_p, weight) else: # print ( calc_delta(points[i-1], points[i], points[i+1]) ) wrap_line(points[i-1], points[i], points[i+1], points[i+2], weight)
-
and thanks to @gferreira who helped me getting the initial bits!
-
Thanks for sharing this!—I'll have a look. I agree that Crouwel used that beveled join pretty consistently. It's just that the underlying logic of the letterforms—the grid of nodes, the segments used to make up the glyph paths—is independent of how the strokes are styled. (Thus he had for example a version of the alphabet with dots in the dimensions of his columns and rows.)
-
@jo good times!
-
@jo Johannes, thanks again for posting your code. I'm off to a promising start—the code is handling the 90° bends perfectly and capping the ends correctly; these paths all have 3 or more points to them. But it's not handling the 2-point segments correctly, as you can see here (the red circles mark the node locations in the grid). I'm digging into the code now, but in case you have any ideas … ?
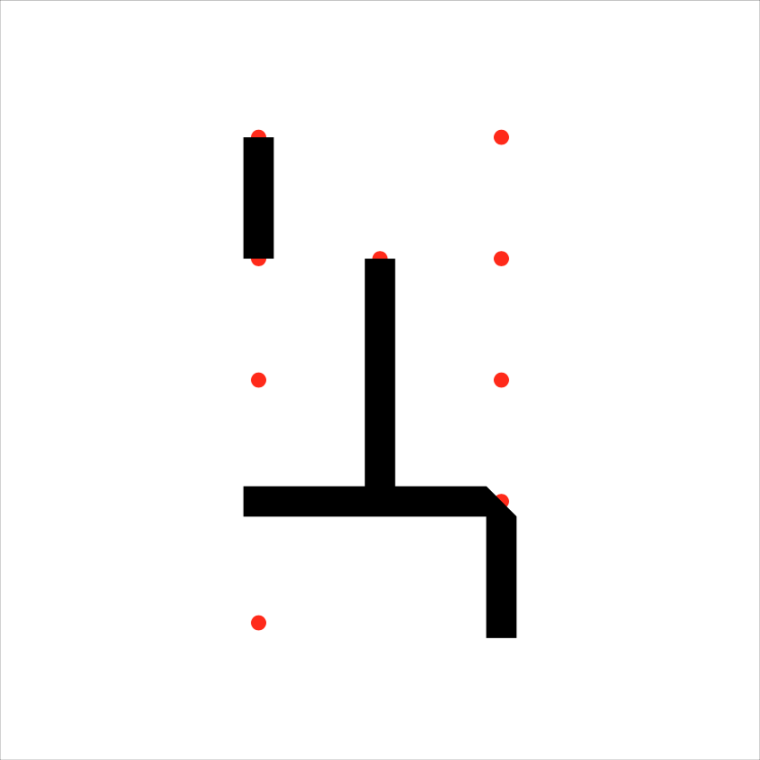
-
I can confirm the sq_cap toggle does work and affects the polygon drawn around the bent paths, but not the two-segment paths.
-
Figured it out, seems obvious: the <if len(points) == 2:> option wasn't adjusting for the square cap. Just took some adapting the code and it all works great, now. Thanks again!
-
@mauricemeilleur sorry. I made the changes and updated the post. Only after implementing the changes in my local version did I realize that i forgot to adapt the
len(points) == 2option. but great you figured it out anyway,
good luck!
-
The last thing will be to provide for the case where the points are in a continuous chain, like the <o>. I'm pretty sure I know what to do, and it shouldn't be that hard, but I have some other problems with the Crouwel code to fix first (all to do with graphing and finding valid paths—this whole project is forcing me to teach myself the basics of computer science as I go). I'll post the revised and extended code here when it's done.